какой знак получается при делении отрицательного числа на отрицательное
Деление отрицательных чисел
Как выполнять деление отрицательных чисел легко понять, вспомнив, что деление — это действие, обратное умножению.
Если « a » и « b » положительные числа, то разделить число « a » на число « b », значит найти такое число « с », которое при умножении на « b » даёт число « a ».
Данное определение деления действует для любых рациональных чисел, если делители отличны от нуля.
Поэтому, например, разделить число « −15 » на число 5 — значит, найти такое число, которое при умножении на число 5 даёт число « −15 ». Таким числом будет « −3 », так как
Примеры деления рациональных чисел.
Из примеров видно, что частное двух чисел с одинаковыми знаками — число положительное (примеры 1, 2), а частное двух чисел с разными знаками— число отрицательное (примеры 3, 4).
Правила деления отрицательных чисел
Чтобы найти модуль частного, нужно разделить модуль делимого на модуль делителя.
Итак, чтобы разделить два числа с одинаковыми знаками, надо:
Примеры деления чисел с одинаковыми знаками:
Чтобы разделить два числа с разными знаками, надо:
Примеры деления чисел с разными знаками:
Для определения знака частного можно также пользоваться следующей таблицей.
Правило знаков при делении
При вычислении «длинных» выражений, в которых фигурируют только умножение и деление, пользоваться правилом знаков очень удобно. Например, для вычисления дроби
Можно обратить внимание, что в числителе два знака «минус», которые при умножении дадут «плюс». Также в знаменателе три знака «минус», которые при умножении дадут «минус». Поэтому в конце результат получится со знаком «минус».
Сокращение дроби (дальнейшие действия с модулями чисел) выполняется также, как и раньше:
Частное от деления нуля на число, отличное от нуля, равно нулю.
Все известные ранее правила деления на единицу действуют и на множество рациональных чисел.
Зависимости между результатами умножения и деления, известные для положительных чисел, сохраняются и для всех рациональных чисел (кроме числа нуль):
Данные зависимости используются для нахождения неизвестного множителя, делимого и делителя (при решении уравнений), а также для проверки результатов умножения и деления.
Пример нахождения неизвестного.
Знак «минус» в дробях
Разделим число « −5 » на « 6 » и число « 5 » на « −6 ».
Напоминаем, что черта в записи обыкновенной дроби — это тот же знак деления, поэтому можно записать частное каждого из этих действий в виде отрицательной дроби.
Таким образом знак «минус» в дроби может находиться:
При записи отрицательных дробей знак «минус» можно ставить перед дробью, переносить его из числителя в знаменатель или из знаменателя в числитель.
Это часто используется при выполнении действий с дробями, облегчая вычисления.
Пример. Обратите внимание, что после вынесения знака «минуса» перед скобкой мы из большего модуля вычитаем меньший по правилам сложения чисел с разными знаками.
Используя описанное свойство переноса знака в дроби, можно действовать, не выясняя, модуль какого из данных дробных чисел больше.
Как разделить отрицательные числа?
Деление отрицательных. Как делить два отрицательных числа. Как разделить, если одно число отрицательное. И разделим отрицательные числа на калькуляторе!
Для деления отрицательных чисел существует только два пункта правил!
О делении отрицательных.
Правило деления отрицательных чисел.
Правила деления отрицательных аналогично умножению, только отличие в знаке.
1). Когда делимое и делить отрицательные
Первый пункт правил деления отрицательных чисел звучит так : «если делимое a и делитель b » отрицательные, то минус на минус дает плюс, т.е. результат(частное с) будет положительным:
2). Когда при делении только одно число отрицательное
Как разделить отрицательные числа.
Заменяем наши буквы на числа и получим пример деления отрицательных чисел.
(-15) : (-12) = 15 : 12 = 1.25
Как разделить отрицательные числа на калькуляторе.
Как и в предыдущем пункте заменяем буквенные значения на числовые.
Как разделить отрицательные числа на калькуляторе.
Следующим пунктом, мы разделим два отрицательных числа на калькуляторе
Набираем делимое 12.
Набираем делитель : 15.
Меняем знак на отрицательный, кнопкой плюс/минус : «±».
Получаем результат деления двух отрицательных чисел.
Как разделить отрицательное на положительное на калькуляторе.
Делим отрицательные на калькуляторе, когда только одно число отрицательное:
Набираем делимое 12.
Набираем делитель : 15.
Получаем результат деления двух отрицательных чисел, когда лишь одно число отрицательное.
Деление отрицательных чисел, правило, примеры.
В центре внимания этой статьи находится деление отрицательных чисел. Сначала дано правило деления отрицательного числа на отрицательное, приведено его обоснования, а после этого приведены примеры деления отрицательных чисел с подробным описанием решений.
Навигация по странице.
Правило деления отрицательных чисел
Правило деления отрицательных чисел следующее: частное от деления одного отрицательного числа на другое равно частному от деления модуля числителя на модуль знаменателя.
Очевидно, что данное правило сводит деление отрицательных чисел к делению положительных чисел (модулей делимого и делителя), следовательно, результатом деления отрицательного числа на отрицательное число будет положительное число.
Сразу отметим, что это правило также можно применять при делении чисел с разными знаками.
А это правило позволяет от деления отрицательных чисел перейти к умножению.
Осталось рассмотреть применение рассмотренных правил деления отрицательных чисел при решении примеров.
Примеры деления отрицательных чисел
Разберем примеры деления отрицательных чисел. Начнем с простых случаев, на которых отработаем применение правила деления.
(−18):(−3)=6 и 
При делении дробных рациональных чисел удобнее всего работать с обыкновенными дробями. Но, если удобно, то можно делить и конечные десятичные дроби.
Разберем оба подхода.
А теперь покажем, как бы выглядело решение, если бы мы решили осуществить перевод десятичных дробей в обыкновенные. Так как 



Полученные результаты 0,016 и 



Также стоит сказать, что если делимое и (или) делитель является иррациональным числом, заданным как корень, степень, логарифм, синус и т.п., то результат деления часто записывается в виде числового выражения. А значение этого выражения вычисляется лишь в случае надобности.
Разделите отрицательное число −0,5 на отрицательное число 

Рекомендуем продолжить изучение темы материалом статьи деление действительных чисел.
 masterok
masterok
Мастерок.жж.рф
Хочу все знать
А давайте зададимся.
Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.
В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Рассмотрим для примера уравнение 7x – 17 = 2x – 2. Его можно решать так: перенести члены с неизвестным в левую часть, а остальные — в правую, получится 7x – 2x = 17 – 2, 5x = 15, x = 3. При таком решении нам даже не встретились отрицательные числа.
Но можно было случайно сделать и по-другому: перенести слагаемые с неизвестным в правую часть и получить 2 – 17 = 2x – 7x, (–15) = (–5)x. Чтобы найти неизвестное, нужно разделить одно отрицательное число на другое: x = (–15)/(–5). Но правильный ответ известен, и остается заключить, что (–15)/(–5) = 3.
Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции. Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики).
В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец.
Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.
Кольцом называется множество с двумя бинарными операциями (т. е. в каждой операции задействованы два элемента кольца), которые по традиции называют сложением и умножением, и следующими аксиомами:
-сложение элементов кольца подчиняется переместительному (A + B = B + A для любых элементов A и B) и сочетательному (A + (B + C) = (A + B) + C) законам; в кольце есть специальный элемент 0 (нейтральный элемент по сложению) такой, что A + 0 = A, и для любого элемента A есть противоположный элемент (обозначаемый (–A)), что A + (–A) = 0;
-умножение подчиняется сочетательному закону: A·(B·C) = (A·B)·C;
сложение и умножение связаны такими правилами раскрытия скобок: (A + B)·C = A·C + B·C и A·(B + C) = A·B + A·C.
Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец.
Теперь докажем, что для любых элементов A и B произвольного кольца верно, во-первых, (–A)·B = –(A·B), а во-вторых (–(–A)) = A. Из этого легко следуют утверждения про единицы: (–1)·1 = –(1·1) = –1 и (–1)·(–1) = –((–1)·1) = –(–1) = 1.
Для этого нам потребуется установить некоторые факты. Сперва докажем, что у каждого элемента может быть только один противоположный. В самом деле, пусть у элемента A есть два противоположных: B и С. То есть A + B = 0 = A + C. Рассмотрим сумму A + B + C. Пользуясь сочетательным и переместительным законами и свойством нуля, получим, что, с одной стороны, сумма равна B: B = B + 0 = B + (A + C) = A + B + C, а с другой стороны, она равна C: A + B + C = (A + B) + C = 0 + C = C. Значит, B = C.
Заметим теперь, что и A, и (–(–A)) являются противоположными к одному и тому же элементу (–A), поэтому они должны быть равны.
Первый факт получается так: 0 = 0·B = (A + (–A))·B = A·B + (–A)·B, то есть (–A)·B противоположно A·B, значит, оно равно –(A·B).
Чтобы быть математически строгими, объясним еще, почему 0·B = 0 для любого элемента B. В самом деле, 0·B = (0 + 0) B = 0·B + 0·B. То есть прибавление 0·B не меняет сумму. Значит, это произведение равно нулю.
А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения.
Остаток от деления отрицательных чисел
В этой статье я расскажу о том, как правильно находить остаток от деления отрицательных чисел. Этой теме, к сожалению, уделяется очень мало внимания в школе, хотя для понимания учеником базовых основ математики она чрезвычайно важна. Именно поэтому, как репетитор по математике, на своих занятиях я разбираю это материал с учениками во всех подробностях. Это значительно упрощает дальнейшую подготовку к ЕГЭ, ОГЭ, вступительным экзаменам и олимпиадам по математике.
Итак, приступим. Чтобы разделить друг на друга два целых числа с остатком, нужно воспользоваться следующей теоремой:
Для любых целых чисел 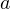 и и 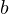 , причём , причём 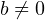 , найдётся единственная пара целых чисел , найдётся единственная пара целых чисел 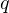 и и  , таких что , таких что 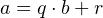 , где , где 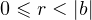 . . |
Здесь 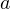
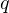


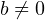
Звучит довольно сложно, но на самом деле в этой теореме нет ничего сложного. Чтобы во всём разобраться, перейдём к примерам.
Примеры нахождения остатка от деления отрицательных чисел
Пример 1. Деление с остатком положительного целого числа на положительное целое число.
Допустим, что требуется разделить с остатком 27 на 4. Вопрос состоит в том, сколько раз число 4 содержится в числе 27? Но мы знаем, что нет такого целого числа, на которое можно умножить 4, чтобы получить 27. Поэтому вопрос нужно переформулировать. На какое число нужно умножить 4, чтобы получить число, максимально близкое к 27, но не превзойти его? Очевидно, что это число 6. Если 4 умножить на 6, то получится 24. До исходного делимого 27 не хватает 3. Следовательно, остаток от деления 27 на 4 составляет 3:
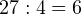
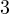
Пример 2. Деление с остатком отрицательного целого числа на положительное целое число.
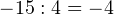
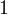
Пример 3. Деление положительного целого числа на отрицательное целое число.
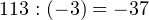
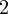
Пример 4. Деление с остатком отрицательного целого числа на отрицательное целое число.
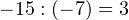
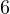
Проверьте, насколько хорошо вы поняли этот урок. Найдите самостоятельно остаток от деления отрицательных чисел:
Свои ответы пишите в комментариях, я их проверю.










 masterok
masterok
