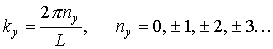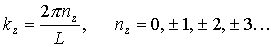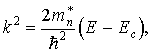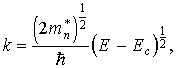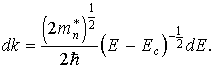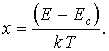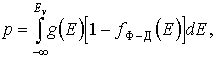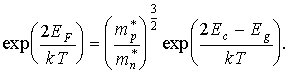при каком значении параметра вырождения а распределения ферми дирака и бозе эйнштейна
При каком значении параметра вырождения а распределения ферми дирака и бозе эйнштейна
3.1. Статистическое описание коллектива частиц.
Функция распределения частиц по состояниям. Фермионы и бозоны
Системы, состоящие из большого количества тождественных частиц, являются предметом изучения статистической физики. Основной особенностью статистических закономерностей является их вероятностный характер. Хорошо известен метод статистического описания коллектива молекул идеального газа. Несмотря на то, что скорость отдельной молекулы газа является величиной случайной в газе, состоящем из большого числа одинаковых молекул, наблюдается определенная закономерность в распределении их по скоростям. Используя методы статистической физики, всегда можно указать, какая доля молекул имеет скорость, заключенную в данном интервале значений.

Таким образом, функция распределения частиц по энергиям есть плотность заполнения данных состояний частицами.
Для молекул идеального газа f(E) известна как функция распределения Максвелла-Больцмана:

Формулу (3.2) называют часто также каноническим распределением или распределением Гиббса. Из этого распределения можно легко получить известное из молекулярной физики распределение Максвелла молекул идеального газа по скоростям теплового движения. Статистика молекул идеального газа исходит из следующих основных положений:
1. Молекулы газа подчиняются законам классической механики.
2. Молекулы газа обладают индивидуальностью, позволяющей отличать их друг от друга. Поэтому, когда две молекулы, находящиеся в разных состояниях меняют местами, это приводит к новому распределению их по состояниям (новому микросостоянию).
3. Предполагается, что все способы распределения равновероятны.
Предположение о том, что электронный газ в металлах подчиняется статистике Максвелла-Больцмана, опровергается рядом экспериментальных результатов. Например, из этого предположения следует, что электроны должны давать вклад в теплоемкость металлов, который примерно на два порядка больше экспериментально наблюдаемой величины. Противоречие снимается, если учитывать квантовые свойства частиц в кристаллах.
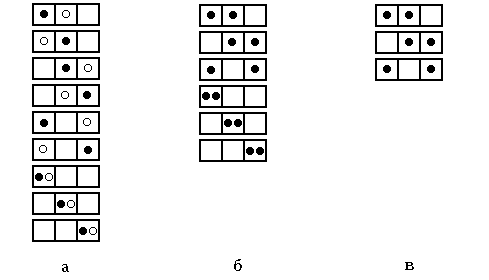
Рис. 3.1. Сравнение различных статистик на примере распределения двух частиц по трем состояниям:
Статистике Бозе-Эйнштейна подчиняются фотоны и фононы, играющие важную роль в физических свойствах твердых тел. Функция распределения Бозе-Эйнштейна имеет вид
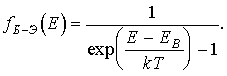
Если полное число частиц не фиксировано, а должно определяться из условия термодинамического равновесия, как это имеет место для фотонов при излучении абсолютно черного тела, или фононов в кристалле, химический потенциал равен нулю. В этом случае формула (3.3) совпадает с формулой Планка, определяющей среднее число фотонов в данном типе колебаний теплового излучения абсолютно черного тела.
3.2. Функция распределения Ферми-Дирака. Уровень Ферми.
Энергия Ферми. Влияние температуры на распределение Ферми-Дирака
Функция распределения Ферми-Дирака, описывающая распределение фермионов по состояниям, имеет следующий вид:
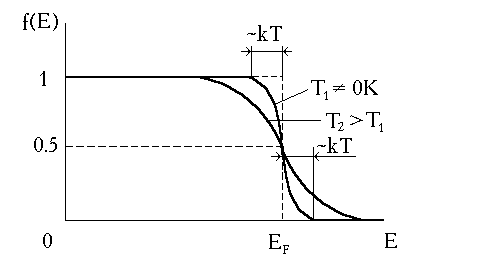
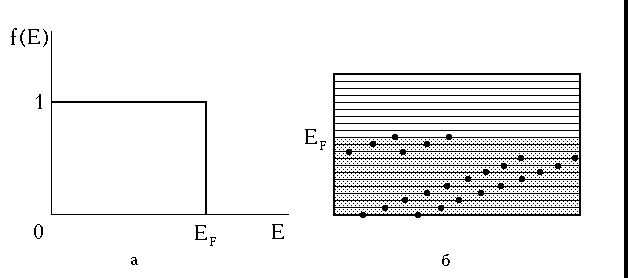
Вид функции распределения Ферми-Дирака при Т = 0К представлен на рис. 3.2,а. На рис. 3.2,б показано распределение электронов по энергетическим уровням в зоне проводимости металла при этой же температуре.
Рис. 3.3. Функция распределения Ферми-Дирака при Т>0K
Рис. 3.2. Функция распределения Ферми-Дирака (а) и распределение электронов в зоне проводимости металла при Т=0К (б)
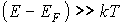
экспонента в знаменателе становится значительно больше единицы в формуле (3.4). В этом случае единицей можно пренебречь и распределение Ферми-Дирака преобразуется к виду
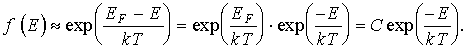
Выражение (3.6) совпадает по форме с функцией распределения Максвелла-Больцмана.
Вероятность того, что некоторый энергетический уровень с энергией Е свободен, т.е. занят дыркой, равна
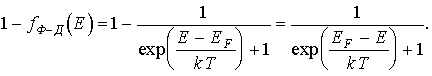
Таким образом, функция распределения Ферми-Дирака для дырок аналогична функции распределения для электронов, если в ней изменить знаки показателей экспонент. Это хорошо согласуется с представлением о том, что дырки являются носителями положительного заряда.
Газ носителей заряда, подчиняющийся статистике Ферми-Дирака, называется вырожденным. Если носители заряда подчиняются статистике Максвелла-Больцмана, то они называются невырожденными.
3.3. Функция плотности состояний электронов и дырок
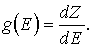
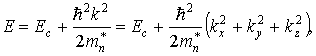
Подставляя значения k 2 и dk в формулу (3.10), получим
Учитывая (3.8), получим окончательное выражение для плотности квантовых состояний электронов у дна зоны проводимости:
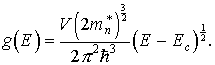
Энергию дырок у потолка валентной зоны можно записать также в виде параболического закона:
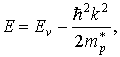
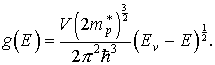
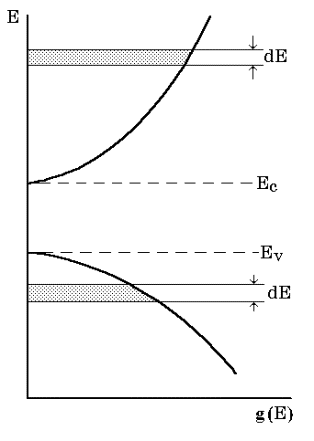
Следует подчеркнуть, что формулы (3.11) и (3.13) справедливы только для состояний вблизи экстремумов энергии, т.е. у дна или потолка энергетической зоны. В средней же части зоны точный вид функции g(E) неизвестен. На рис. 3.4 схематически представлены зависимости плотности квантовых уровней вблизи дна зоны проводимости и потолка валентной зоны.
Рис. 3.4. Плотность уровней в зоне проводимости и в валентной зоне
Площадь заштрихованных областей пропорциональна числу уровней в интервале энергий dE
3.4. Концентрации электронов и дырок в полупроводнике.
Закон действующих масс. Невырожденный газ электронов и дырок
Вычислим концентрацию электронов в зоне проводимости полупроводника. Число электронов dN, находящихся в dZ состояниях энергетической зоны в соответствии с уравнением (3.1) определяется выражением
Учитывая, что dZ = g(E) dE, получим
Общее число электронов в зоне проводимости найдем, проинтегрировав выражение (3.14) в пределах зоны
Преобразуем теперь выражение (3.16) к виду
Произведем замену переменных в подынтегральном выражении
В результате получим
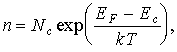
Величину Nc называют эффективной плотностью состояний в зоне проводимости. Это название связано с тем, что полная концентрация электронов, распределенных в действительности в определенном энергетическом интервале в зоне проводимости, такая же, как если бы зона была занята Nc уровнями, обладающими одной и той же энергией Еc.
Тогда концентрация дырок
При условии, что газ дырок невырожденный, получим
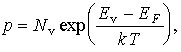
где эффективная плотность состояний в валентной зоне
Перемножая выражения (3.17) и (3.19), получим
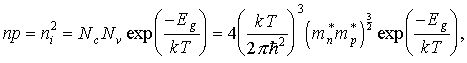
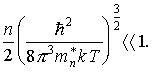
Вопрос о том, является газ носителей заряда в кристалле вырожденным или невырожденным определяется только его концентрацией и температурой. Подстановка численных значений величин, входящих в неравенство (3.22), приводит к выводу о том, что при комнатной температуре (Т
Таким образом, закон действующих масс выполняется для любого невырожденного полупроводника независимо от роли примесей, т.е. в любом невырожденном полупроводнике увеличение концентрации носителей одного знака приводит к уменьшению концентрации носителей противоположного знака. Следует отметить также, что произведение электронной и дырочной концентраций не зависит от положения уровня Ферми.
3.5. Уровень Ферми в полупроводниках
Для собственного полупроводника концентрации электронов и дырок равны (n = p), т.к. каждый электрон, покинувший валентную зону, создает одну дырку. Приравнивая равенства (3.17) и (3.19), получим
Разрешая последнее равенство относительно ЕF, получим
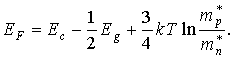
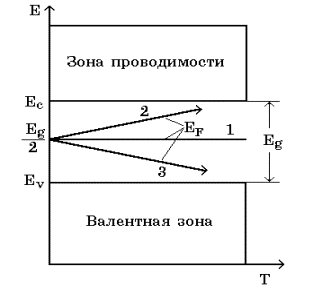
Температурная зависимость положения уровня Ферми в собственном полупроводнике определяется третьим слагаемым в уравнении (3.23). Если эффективная масса дырки в валентной зоне больше эффективной массы электрона в зоне проводимости, то уровень Ферми смещается с повышением температуры ближе к дну зоны проводимости. В противоположном случае уровень Ферми смещается к потолку валентной зоны. Положение уровня Ферми в собственном полупроводнике с изменением температуры схематически показано на рис. 3.5.
Рис. 3.5. Положение уровня Ферми в собственном полупроводнике
Положение уровня Ферми в примесных полупроводниках может быть найдено из условия электронейтральности кристалла. Для донорного полупроводника это условие записывается в виде
Концентрацию электронов на донорных уровнях можно вычислить, умножив концентрацию этих уровней Nd на функцию распределения Ферми-Дирака:
Подстановка в условие электронейтральности (3.24) концентраций электронов (3.17) и дырок (3.19), а также концентрации электронов на донорных уровнях (3.25) приводит к следующему уравнению относительно положения уровня Ферми ЕF :
При подстановке концентрации электронов на донорных уровнях в уравнение (3.24 ) было сделано предположение, что газ электронов примесных атомов невырожденный, что позволило пренебречь единицей в знаменателе формулы (3.25).
Уравнение (3.26) ввиду его сложности обычно в общем виде не решают, а ограничиваются рассмотрением частных случаев. Например, при низких температурах, когда электроны в зоне проводимости появляются в основном за счет переходов с примесных уровней, а концентрация дырок близка к нулю, решение уравнения (3.26) имеет вид

Аналогично можно получить выражение для температурной зависимости уровня Ферми в акцепторном полупроводнике. График этой зависимости схематически приведен на рис. 3.6,б.
3.6. Равновесные и неравновесные носители заряда. Квазиуровни Ферми
Положение уровня Ферми в собственных и примесных полупроводниках связано с концентрацией носителей заряда, установившейсяпри данной температуре в состоянии термодинамического равновесия. Переброс электронов в зону проводимости за счет температурного возбуждения и возникновение в результате этого процесса дырок в валентной зоне называется термической генерацией свободных носителей заряда. Одновременно происходит и обратный процесс: электроны возвращаются в валентную зону, в результате чего исчезают электрон и дырка. Этот процесс называется рекомбинацией носителей заряда. Для количественного описания процессов генерации и рекомбинации носителей заряда в полупроводниках используют понятия скорости генерации, скорости рекомбинации и времени жизни носителей заряда.
Время жизни носителeй t — это среднее время от генерации носителя до его рекомбинации.
Из приведенных выше определений непосредственно следуют следующие соотношения между скоростями рекомбинации электронов Rn и дырок Rp и их временами жизни t n и t p соответственно:
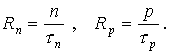
При фиксированной температуре устанавливается термодинамическое равновесие, при котором процессы генерации и рекомбинации взаимно уравновешиваются. Такие носители, находящиеся в тепловом равновесии с кристаллической решеткой, называются равновесными.
Электропроводность полупроводника может быть возбуждена и другими способами, например, облучением светом, действием ионизирующих частиц, электрическим полем, инжекцией носителей через контакт и др. Во всех этих случаях дополнительно к равновесным носителям в полупроводнике возникают носители заряда, которые не будут находиться в состоянии теплового равновесия с кристаллом. Такие носители называются неравновесными.
Общую концентрацию электронов в зоне проводимости n в случае равновесных и неравновесных носителей можно представить в виде
Общая концентрация дырок
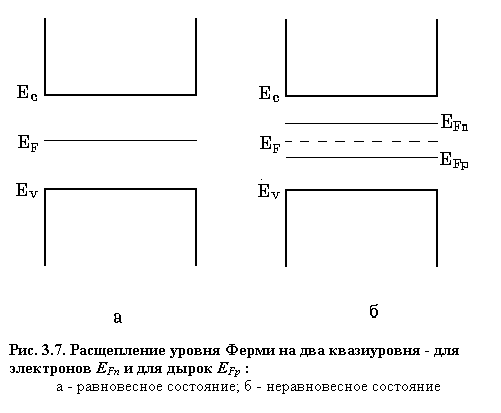
Поскольку распределение Ферми-Дирака справедливо только для состояния термодинамического равновесия, то понятно, что статистика неравновесных носителей должна быть иной. В отсутствие термодинамического равновесия принято вводить два новых параметра распределения EFn для электронов и EFp для дырок. Эти параметры выбираюттаким образом, чтобы для концентраций электронов и дырок при наличии неравновесныхносителей выполнялись уравнения (3.17) и (3.19) соответственно при условии замены EF на EFn для электронов и на EFp для дырок. Величины EFn и EFp называют квазиуровнями Ферми электронов и дырок соответственно. Таким образом, в невырожденных полупроводниках справедливы уравнения
Поскольку при наличии избыточных носителей заряда закон действующих масс не выполняется ( 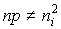
В состоянии термодинамического равновесия квазиуровни Ферми совпадают с равновесным уровнем Ферми EF. Чем выше концентрация неравновесных носителей заряда, тем дальше отстоят квазиуровниФерми от уровня Ферми. Из уравнений (3.31), (3.32), (3.17) и (3.19) следует
Неравновесные носители играют важную роль в работе полупроводниковых приборов.
Понятие о квантовой статистике Бозе — Эйнштейна и Ферми — Дирака
Идеальный газ из бозонов — бозе-газ — описывается квантовой статистикой Бозе — Эйнштейна(Д. Бозе (1858—1937)—индийский физик). Распределение бозонов по энергиям вытекает из так называемого большого канонического распределения Гиббса (с переменным числом частиц) при условии, что число тождественных бозонов в данном квантовом состоянии может быть любым (см. § 227):
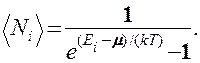
Это распределение называется распределением Бозе — Эйнштейна. Здесь 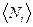
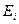
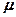
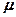
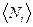
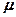
Идеальный газ из фермионов — ферми-газ — описывается квантовой статистикой Ферми — Дирака (Э. Ферми (1901 — 1954) — итальянский физик). Распределение фермионов по энергиям имеет вид
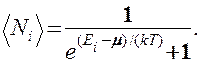
где 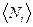
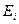
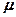
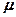
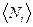
Если 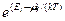
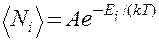
(ср. с выражением (44.4)), где
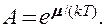
Таким образом, при высоких температурах оба «квантовых» газа ведут себя подобно классическому газу.
Система частиц называется вырожденной, если ее свойства существенным образом отличаются от свойств систем, подчиняющихся классической статистике. Поведение как бозе-газа, так и ферми-газа отличается от классического газа, они являются вырожденными газами. Вырождение газов становится существенным при весьма низких температурах и больших плотностях. Параметром вырождения называется величина А. При А
Температурой вырождения 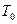
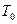
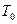
Бозе — Эйнштейна и Ферми — Дирака



Идеальный газ из бозонов — бозе-газ — описывается квантовой статистикой Бозе — Эйнштейна*. Распределение бозонов по энергиям вытекает из так называемого большого канонического распределения Гиббса (с переменным числом частиц) при условии, что число тождественных бозонов в данном квантовом состоянии может быть любым (см. § 227):
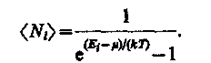
Это распределение называется распределением Боэе — Эйнштейна. Здесь áNiñ — среднее число бозонов в квантовом состоянии с энергией Ei, k — постоянная Больцмана, T—термодинамическая температура, m —химический потенциал; mне зависит от энергии, а определяется только температурой и плотностью числа частиц. Химический потенциал находится обычно из условия, что сумма всех áNiñ равна полному числу частиц в системе. Здесь m £ 0, так как иначе среднее число частиц в данном квантовом состоянии отрицательно, что не имеет физического смысла. Он определяет изменение внутренней энергии системы при добавлении к ней одной частицы при условии, что все остальные величины, от которых зависит внутренняя энергия (энтропия, объем), фиксированы.
Идеальный газ из фермионов — фермн-газ — описывается квантовой статистикой Ферми — Дирака**. Распределение фермионов по энергиям имеет вид
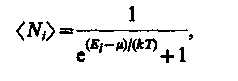
где áNiñ — среднее число фермионов в квантовом состоянии с энергией Еi, m— химический потенциал. В отличие от (235.1) mможет иметь положительное значение (это не приводит к отрицательным значениям чисел áNiñ). Это распределение называется распределением Ферми — Дирака.

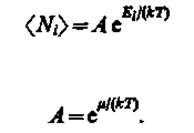
Таким образом, при высоких температурах оба «квантовых» газа ведут себя подобно классическому газу.
Система частиц называется вырожденной, если ее свойства существенным образом отличаются от свойств систем, подчиняющихся классической статистике. Поведение как бозе-газа, так и ферми-газа отличается от классического газа, они являются вырожденными газами. Вырождение газов становится существенным при весьма низких температурах и больших плотностях. Параметром вырождения называется величина А. При A > T0, то поведение системы частиц (газа) описывается классическими законами.