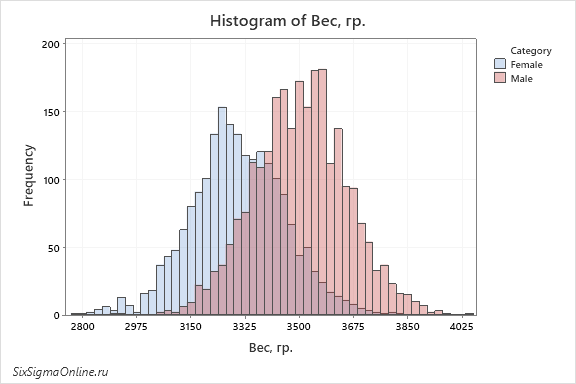
распределение какого параметра показано на диаграмме
Типичные распределения вероятности: шпаргалка data scientist-а
У data scientist-ов сотни распределений вероятности на любой вкус. С чего начать?
Data science, чем бы она там не была – та ещё штука. От какого-нибудь гуру на ваших сходках или хакатонах можно услышать:«Data scientist разбирается в статистике лучше, чем любой программист». Прикладные математики так мстят за то, что статистика уже не так на слуху, как в золотые 20е. У них даже по этому поводу есть своя несмешная диаграмма Венна. И вот, значит, внезапно вы, программист, оказываетесь совершенно не у дел в беседе о доверительных интервалах, вместо того, чтобы привычно ворчать на аналитиков, которые никогда не слышали о проекте Apache Bikeshed, чтобы распределённо форматировать комментарии. Для такой ситуации, чтобы быть в струе и снова стать душой компании – вам нужен экспресс-курс по статистике. Может, не достаточно глубокий, чтобы вы всё понимали, но вполне достаточный, чтобы так могло показаться на первый взгляд.
Вероятностные распределения – это основа статистики, так же как структуры данных – основа computer science. Если хотите говорить языком data scientist-а – надо начинать с их изучения. В принципе можно, если повезёт, делать простые анализы, используя R или scikit-learn вообще без понимания распределений, так же как можно написать программу на Java без понимания хэшфункций. Но рано или поздно это закончится слезами, ошибками, ложными результатами или — гораздо хуже – охами и выпученными глазами от старших статистиков.
Существуют сотни различных распределений, некоторые из которых на слух звучат как чудовища средневековых легенд, типа Muth или Lomax. Тем не менее, на практике более-менее часто используются около 15. Каковы они, и какие умные фразы о них требуется запомнить?
Итак, что такое распределение вероятности?
Всё время что-то происходит: кидаются кубики, идёт дождь, подъезжают автобусы. После того, как это что-то произошло, можно быть уверенным в некотором исходе: кубики выпали на 3 и 4, выпало 2.5 см дождя, автобус подъехал через 3 минуты. Но до этого момента мы можем говорить только о том, насколько каждый исход возможен. Распределения вероятности описывают то, как мы видим вероятность каждого исхода, что, зачастую, гораздо интереснее, чем знать только один, наиболее возможный, исход. Распределения бывают разных форм, но строго одного размера: сумма всех вероятностей в распределении — всегда 1.
Например, подбрасывание правильной монетки имеет два исхода: она упадёт либо орлом, либо решкой (предполагая, что она не приземлится на ребро и её не стащит в воздухе чайка). Перед броском мы верим, что с шансом 1 к 2 или с вероятностью 0.5 она упадёт орлом. Точно так же, как и решкой. Это распределение вероятности двух исходов броска, и, если вы внимательно прочитали это предложение, то вы уже поняли распределение Бернулли.
Несмотря на экзотические названия, распространённые распределения связаны друг с другом достаточно интуитивными и интересными способами, позволяющими легко их вспоминать и уверенно о них рассуждать. Некоторые естественно следуют, например, из распределения Бернулли. Время показать карту этих связей.
Распечатайте, отрежьте по пунктирной линии и носите с собой в кошельке. Это — ваш путеводитель в стране распределений и их родственников.
Бернулли и равномерное
Вы уже встретились с распределением Бернулли выше, с двумя исходами – орлом или решкой. Представьте его теперь как распределение над 0 и 1, 0 – орёл, 1 – решка. Как уже понятно, оба исхода равновероятны, и это отражено на диаграмме. ФПР Бернулли содержит две линии одинаковой высоты, представляющие 2 равновероятных исхода: 0 и 1 соответственно.
Распределение Бернулли может представлять и неравновероятные исходы, типа броска неправильной монетки. Тогда вероятность орла будет не 0.5, а какая-то другая величина p, а вероятность решки – 1-p. Как и многие другие распределения, это на самом деле целое семейство распределений, задаваемых определёнными параметрами, как p выше. Когда будете думать «Бернулли» – думайте про «бросок (возможно, неправильной) монетки».
Отсюда весьма небольшой шаг до того, чтобы представить распределение поверх нескольких равновероятных исходов: равномерное распределение, характеризуемое плоской ФПР. Представьте правильный игральный кубик. Его исходы 1-6 равновероятны. Его можно задать для любого количества исходов n, и даже в виде непрерывного распределения.
Думайте о равномерном распределении как о «правильном игральном кубике».
Биномиальное и гипергеометрическое
Биномиальное распределение можно представить как сумму исходов тех вещей, которые следуют распределению Бернулли.
Киньте честную монету два раза – сколько раз будет орёл? Это число, подчиняющееся биномиальному распределению. Его параметры – n, число испытаний, и p – вероятность «успеха» (в нашем случае – орла или 1). Каждый бросок – распределённый по Бернулли исход, или испытание. Используйте биномиальное распределение, когда считаете количество успехов в вещах типа броска монеты, где каждый бросок не зависит от других и имеет одинаковую вероятность успеха.
Или представьте урну с одинаковым количество белых и чёрных шаров. Закройте глаза, вытащите шар, запишите его цвет и верните назад. Повторите. Сколько раз вытащился чёрный шар? Это число также подчиняется биномиальному распределению.
Эту странную ситуацию мы представили, чтобы было легче понять смысл гипергеометрического распределения. Это распределение того же числа, но в ситуации если бы мы не возвращали шары обратно. Оно, безусловно, двоюродный брат биномиального распределения, но не такое же, так как вероятность успеха изменяется с каждым вытащенным шаром. Если количество шаров достаточно велико по сравнению с количеством вытаскиваний – то эти распределения практически одинаковы, так как шанс успеха изменяется с каждым вытаскиванием крайне незначительно.
Когда где-то говорят о вытаскивании шаров из урн без возврата, практически всегда безопасно ввернуть «да, гипергеометрическое распределение», потому что в жизни я ещё не встречал никого, кто реально наполнял бы урны шарами и потом вытаскивал их и возвращал, или наоборот. У меня даже знакомых нет с урнами. Ещё чаще это распределение должно всплывать при выборе значимого подмножества некоторой генеральной совокупности в качестве выборки.
Тут может быть не очень понятно, а раз туториал и экспресс-курс для новичков — надо бы разъяснить. Генеральная совокупность — есть нечто, что мы хотим статистически оценить. Для оценки мы выбираем некоторую часть (подмножество) и производим требуемую оценку на ней (тогда это подмножество называется выборкой), предполагая, что для всей совокупности оценка будет похожей. Но чтобы это было верно, часто требуются дополнительные ограничения на определение подмножества выборки (или наоборот, по известной выборке нам надо оценить, описывает ли она достаточно точно совокупность).
Практический пример — нам нужно выбрать от компании в 100 человек представителей для поездки на E3. Известно, что в ней 10 человек уже ездили в прошлом году (но никто не признаётся). Сколько минимум нужно взять, чтобы в группе с большой вероятностью оказался хотя бы один опытный товарищ? В данном случае генеральная совокупность — 100, выборка — 10, требования к выборке — хотя бы один, уже ездивший на E3.
В википедии есть менее забавный, но более практичный пример про бракованные детали в партии.
Пуассон
Что насчёт количества заказчиков, звонящих по горячей линии в техподдержку каждую минуту? Это исход, чьё распределение на первый взгляд биномиальное, если считать каждую секунду как испытание Бернулли, в течение которой заказчик либо не позвонит (0), либо позвонит (1). Но электроснабжающие организации прекрасно знают: когда выключают электричество – за секунду могут позвонить двое или даже больше сотни людей. Представить это как 60000 миллисекундных испытаний тоже не поможет – испытаний больше, вероятность звонка в миллисекунду меньше, даже если не учитывать двух и более одновременно, но, технически – это всё ещё не испытание Бернулли. Тем не менее, срабатывает логическое рассуждение с переходом к бесконечности. Пусть n стремится к бесконечности, а p – к 0, и так, чтобы np было постоянным. Это как делить на всё более малые доли времени со всё менее малой вероятностью звонка. В пределе мы получим распределение Пуассона.
Так же, как и биномиальное, распределение Пуассона – это распределение количества: количества раз того, как что-то произойдёт. Оно параметризуется не вероятностью p и количеством испытаний n, но средней интенсивностью λ, что, в аналогии с биномиальным, просто постоянное значение np. Распределение Пуассона – то, о чём надо вспоминать, когда идёт речь о подсчёте событий за определённое время при постоянной заданной интенсивности.
Когда есть что-то, типа прихода пакетов на роутер или появления покупателей в магазине или что-то, ожидающее в очереди – думайте «Пуассон».
Геометрическое и отрицательное биномиальное
Из простых испытаний Бернулли появляется другое распределение. Сколько раз монетка выпадет решкой, прежде, чем выпасть орлом? Число решек подчиняется геометрическому распределению. Как и распределение Бернулли, оно параметризуется вероятностью успешного исхода, p. Оно не параметризуется числом n, количеством бросков-испытаний, потому что число неудачных испытаний как раз и есть исход.
Если биномиальное распределение это «сколько успехов», то геометрическое это «Сколько неудач до успеха?».
Отрицательное биномиальное распределение – простое обобщение предыдущего. Это количество неудач до того, как будет r, а не 1, успехов. Поэтому оно дополнительно параметризуется этим r. Иногда его описывают как число успехов до r неудач. Но, как говорит мой лайф-коуч: «Ты сам решаешь, что есть успех, а что — неудача», так что это тоже самое, если при этом не забыть, что вероятность p тоже должна правильной вероятностью успеха или неудачи соответственно.
Если нужна будет шутка для снятия напряжения, можно упомянуть, что биномиальное и гипергеометрическое распределение – это очевидная пара, но и геометрическое и отрицательное биномиальное так же весьма похожи, после чего заявить «Ну и кто же так их все называет, а?»
Экспоненциальное и Вейбула
Снова о звонках в техподдержку: сколько пройдёт до следующего звонка? Распределение этого времени ожидания как будто бы геометрическое, потому что каждая секунда, пока никто не звонит – это как неуспех, до секунды, пока, наконец, звонок не произойдёт. Количество неудач –это как количество секунд, пока никто не звонил, и это практически время до следующего звонка, но «практически» нам недостаточно. Суть в том, что это время будет суммой целых секунд, и, таким образом, не получится посчитать ожидание внутри этой секунды до непосредственно звонка.
Ну и, как и раньше, переходим в геометрическом распределении к пределу, относительно временных долей – и вуаля. Получаем экспоненциальное распределение, которое точно описывает время до звонка. Это непрерывное распределение, первое такое у нас, потому что исход не обязательно в целых секундах. Как и распределение Пуассона, оно параметризуется интенсивностью λ.
Повторяя связь биномиального с геометрическим, Пуассоновское «сколько событий за время?» связано с экспоненциальным «сколько до события?». Если есть события, количество которых на единицу времени подчиняется распределению Пуассона, то время между ними подчиняется экспоненциальному распределению с тем же параметром λ. Это соответствие между двумя распределениями необходимо отмечать, когда обсуждается любое из них.
Экспоненциальное распределение должно приходить на ум при размышлении о «времени до события», возможно, «времени до отказа». По факту, это такая важная ситуация, что существуют более обобщённые распределения чтобы описать наработку-на-отказ, типа распределения Вейбула. В то время, как экспоненциальное распределение подходит, когда интенсивность — износа, или отказов, например – постоянна, распределение Вейбула может моделировать увеличивающуюся (или уменьшающуюся) со временем интенсивность отказов. Экспоненциальное, в общем-то, частный случай.
Думайте «Вейбул» когда разговор заходит о наработке-на-отказ.
Нормальное, логнормальное, Стьюдента и хи-квадрат
Нормальное, или гауссово, распределение, наверное, одно из важнейших. Его колоколообразная форма узнаётся сразу. Как и e, это особенно любопытная сущность, которая проявляется везде, даже из внешне самых простых источников. Возьмите набор значений, подчиняющихся одному распределению – любому! – и сложите их. Распределение их суммы подчиняется (приблизительно) нормальному распределению. Чем больше вещей суммируется – тем ближе их сумма соответствует нормальному распределению (подвох: распределение слагаемых должно быть предсказуемым, быть независимым, оно стремится только к нормальному). То, что это так, несмотря на исходное распределение – это потрясающе.
Меня удивило, что автор не пишет про необходимость сопоставимого масштаба суммируемых распределений: если одно существенно доминирует надо остальными — сходиться будет крайне плохо. И, в общем-то, абсолютная взаимная независимость необязательна, достаточна слабая зависимость.
Ну сойдёт, наверное, для вечеринок, как он написал.
Это называется «центральная предельная теорема», и надо знать, что это, почему так названо и что означает, иначе моментально засмеют.
В её разрезе, нормальное связано со всеми распределениями. Хотя, в основном, его связывают с распределениями всяких сумм. Сумма испытаний Бернулли следует биномиальному распределению и, с увеличением количества испытаний, это биномиальное распределение становится всё ближе в нормальному распределению. Аналогично и его двоюродный брат – гипергеометрическое распределение. Распределение Пуассона – предельная форма биномиального – так же приближается к нормальному с увеличением параметра интенсивности.
Исходы, которые подчиняются логнормальному распределению, дают значения, логарифм которых нормально распределён. Или по-другому: экспонента нормально распределённого значения логнормально распределена. Если суммы – нормально распределены, то запомните так же, что произведения распределены логнормально.
t-Распределение Стьюдента – это основа t-теста, который многие нестатистики изучают в других областях. Оно используется для предположений о среднем нормального распределения и так же стремится к нормальному распределению с увеличением своего параметра. Отличительная особенность t-распределения – его хвосты, которые толще, чем у нормального распределения.
Если толстохвостый анекдот недостаточно раскачал вашего соседа – переходите в довольно забавной байке про пиво. Больше 100 лет назад Гиннесс использовал статистику, чтобы улучшить свой стаут. Тогда Вильям Сили Госсет и изобрёл полностью новую статистическую теорию для улучшенного выращивания ячменя. Госсет убедил босса, что другие пивовары не поймут, как использовать его идеи, и получил разрешение на публикацию, но под псевдонимом «Стьюдент». Самое известное достижение Госсета – как раз это самое t-распределение, которое, можно сказать, названо в честь него.
Наконец, распределение хи-квадрат – распределение сумм квадратов нормально-распределенных величин. На этом распределении построен тест хи-квадрат, который сам основан на сумме квадратов разниц, которые должны быть нормально распределены.
Гамма и бета
В этом месте, если вы уже заговорили о чём-то хи-квадратном, разговор начинается всерьёз. Вы уже, возможно, говорите с настоящими статистиками, и, наверное, стоит уже откланиваться, поскольку могут всплыть вещи типа гамма-распределения. Это обобщение и экспоненциального, и хи-квадрат распределения. Как и экспоненциальное распределение, оно используется для сложных моделей времен ожидания. Например, гамма-распределение появляется, когда моделируется время до следующих n событий. Оно появляется в машинном обучении как «сопряжённое априорное распределение» к парочке других распределений.
Не вступайте в разговор об этих сопряжённых распределениях, но если всё-таки придётся, не забудьте сказать о бета-распределении, потому что оно сопряжённое априорное к большинству упомянутых здесь распределений. Data-scientist-ы уверены, что оно именно для этого и сделано. Упомяните об этом ненароком и идите к двери.
Начало мудрости
Распределения вероятности — это то, о чём нельзя знать слишком много. По настоящему заинтересованные могут обратиться к этой супердетализированной карте всех распределений вероятности. Надеюсь, этот шуточный путеводитель даст вам уверенность казаться «в теме» в современной технокультуре. Или, по крайней мере, способ с высокой вероятностью определить, когда надо идти на менее ботанскую вечеринку.
Шон Овен – директор Data Science в Cloudera, Лондон. До Клаудеры он основал Myrrix Ltd. (сейчас проект Oryx) для коммерционализации широкомасштабных рекомендательных систем в реальном времени на Hadoop. Он так же контрибьютор Apache Spark и соавтор O’Reilly Media’s Advanced Analytics with Spark
Распределение какого параметра показано на диаграмме
Гистограмма – это один из тех немногих способов графического представления данных, доступность и легкость восприятия которого не вызывает сомнения. Она прекрасно подходит для описания больших массивов данных, равно как и для характеристики небольшого числового ряда.
Гистограммы без преувеличения являются одним из наиболее важных инструментов анализа данных в проектах шести сигм. Представление результатов наблюдений с их помощью позволяет исследователю оценить ряд статистических показателей, сделать выводы о функции распределения и определить возможные отклонения, а также сравнить два набора данных (в частности, результаты до и после произведенных действий или внедрения проекта). Во всем этом и множестве других полезных свойствах гистограмм попытаемся разобраться в этой статье.
Информации собрано немало, поэтому для удобства навигации вся статья поделена на разделы. Если вы ищете что-то конкретное, то можно перейти непосредственно к интересующей части по ссылке. Ну а если такой информации не нашлось, обязательно оставьте отзыв в комментариях под публикацией.
Содержание:
Что такое гистограмма?
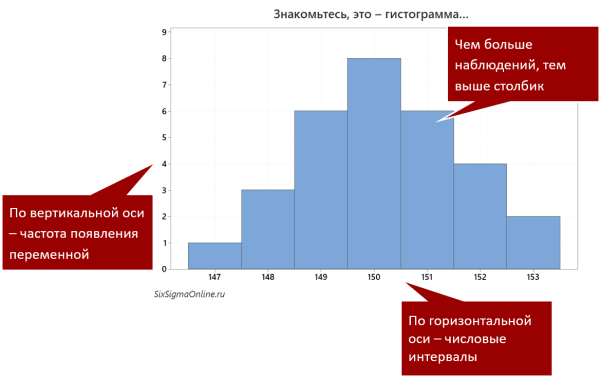
Гистограммой называют двухмерный график, по горизонтальной оси которого откладываются переменные или числовые интервалы, а по вертикальной – частота появления переменной (в заданном интервале).
Чаще всего гистограмма состоит из прямоугольников с шириной, равной величине интервала, и площадью, пропорциональной соответствующей частоте возникновения переменной. Доля всех значений в определенном интервале гистограммы равна его площади (вся площадь гистограммы принимается равной единице, или 100%). Площадь интервала, соответственно, определяет вероятность того, что следующее наблюдение попадет в заданный диапазон результатов. Таким образом, самый высокий столбик гистограммы отвечает интервалу наиболее вероятных результатов.
Другими словами, площадь прямоугольника соответствует количеству значений, которые попадают в определенный интервал: чем больше значений, тем больше площадь – при равных значениях интервалов больший столбик соответствует большему количеству значений.
Отличие от других типов диаграмм и графиков
Забегая наперед, скажу, что гистограмма может принимать самые причудливые формы. Да и для построения этого графика могут применять не только прямоугольники – столбцы, но и кривые, точки, линии… Тем не менее, гистограмма – это также довольно специфический график, и путать его с другими типами диаграммами весьма нерационально.
Чаще всего гистограмму путают со следующими графиками:
Рассмотрим все по порядку.
Отличие гистограммы от столбчатой и/или линейчатой диаграммы
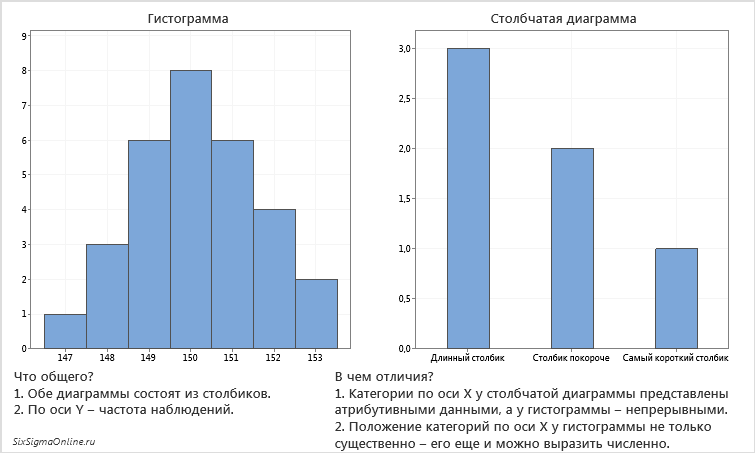
Гистограмма состоит из столбцов, поэтому неудивительно, что ее легко спутать с другой диаграммой, также состоящей из столбцов – столбчатой. Или линейчатой, если говорить о линейках/полосках вместо столбцов. Однако столбчатая и линейчатая диаграммы зачастую отражают количество наблюдений в атрибутивных (или дискретных) категориях, тогда, как у гистограммы по оси Х – непрерывные данные 1 :
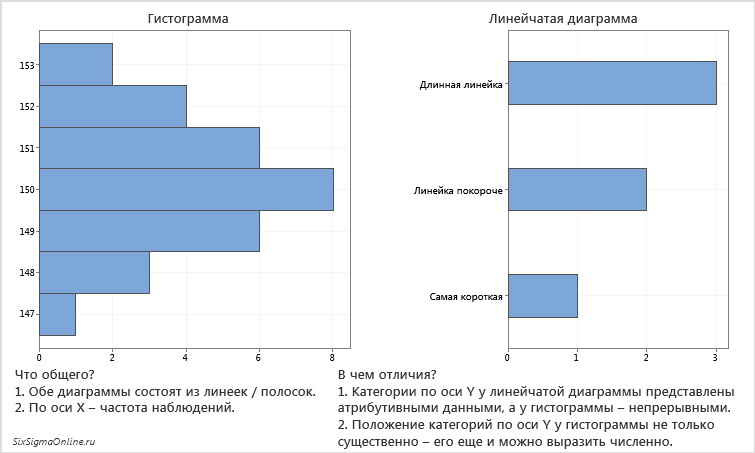
Если диаграммы выше развернуть на 90°, то общие и отличные черты останутся без изменений:
Отдельным пунктом следует выделить диаграмму временного ряда, на которой отложены столбцы вместо точек или линий. У этой диаграммы, как и у гистограммы, по оси X отложены непрерывные данные – дата и/или время. Однако в отличие от гистограммы диаграмма временного ряда показывает наблюдения, упорядоченные во времени, а не распределение значений.
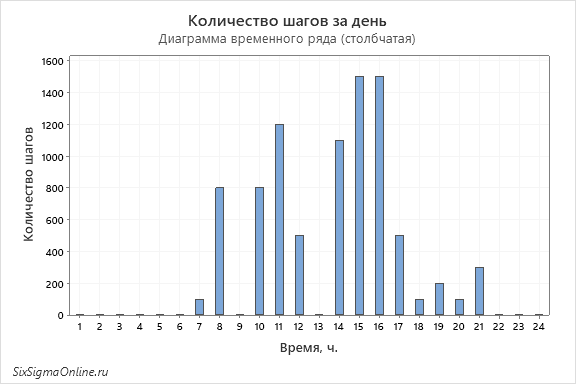
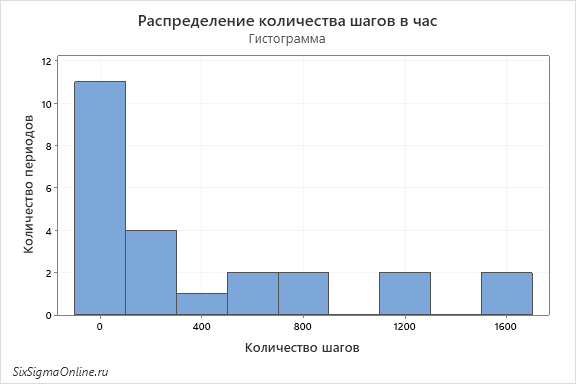
Давайте покажу на примере: сейчас многие носят смарт-часы, которые умеют считать шаги. Допустим, вот так может выглядеть диаграмма временного ряда, если ее сделать столбчатой:
По оси X у нас время в часах, по оси Y – количество шагов в час. Мы видим на диаграмме несколько часов, соответствующих отдыху. В эти часы количество шагов равно 0. Также мы видим несколько часов с большим количеством шагов. К примеру, в период с 14:00 до 16:00 зафиксировано более 1000 шагов в час. Глядя на диаграмму, мы можем сделать вывод о наиболее интенсивных периодах дня и времени отдыха.
Теперь давайте возьмем те же данные и построим гистограмму:
Это совсем другой график, не правда ли? Из него мы не сможем сделать вывод о том, когда в сутках у нас более активный период, а когда менее. Но мы можем наблюдать некое подобие экспоненциального распределения и утверждать только то, что в сутках мы чаще спим, чем ходим по 1600 шагов в час.
Больше о диаграммах временных рядов вы можете узнать из публикации Анализ временных рядов (Time Series Analysis).
Отличие гистограммы от точечной диаграммы (Dotplot)
И гистограммы, и точечные диаграммы отражают распределение переменной – с тем лишь отличием, что гистограммы чаще всего делают это с помощью столбцов, а точечные диаграммы – (только не удивляйтесь) с помощью точек.
Точечные диаграммы дают нам немного больше представления об индивидуальных наблюдениях, так как отражают каждое из них. Гистограммы, в отличие от них, объединяют наблюдения, которые попадают в один интервал, под одним столбцом. Это преимущество, однако, теряется с увеличением количества наблюдений, так как с увеличением количества единичных наблюдений близкие значения также группируют в точки.
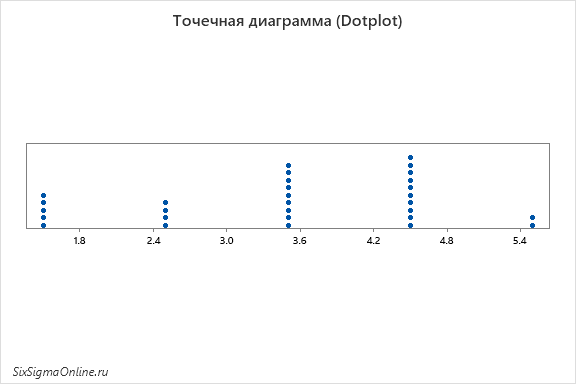
Еще с помощью точечных диаграмм легче заметить “гранулы” – одинаковые значения:
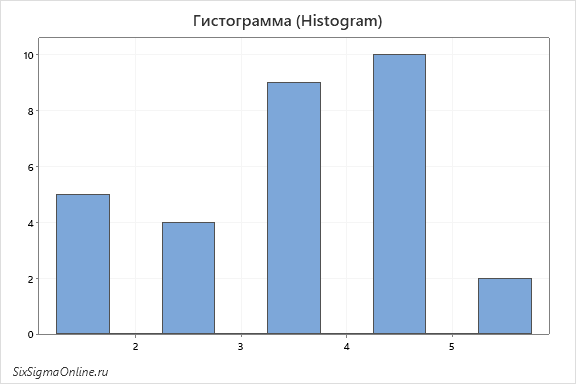
Но чтобы добиться такого же от гистограммы, нужно либо поэкспериментировать с количеством интервалов, либо чтобы “гранулы” наблюдений находились действительно далеко друг от друга:
Больше о точечной диаграмме вы можете узнать из публикации DotPlot в деталях.
Отличие гистограммы от диаграммы “лист и стебель” (Stem-and-Leaf)
Диаграмма “лист и стебель” (Stem-and-Leaf) – это такой себе предшественник гистограммы. Этому графику посвящен отдельный пост на нашем сайте – Что за странный график из листьев и стеблей?, – поэтому вдаваться в детали и описывать его мы не будем. Вместо этого еще раз подчеркнем общие и различные свойства.
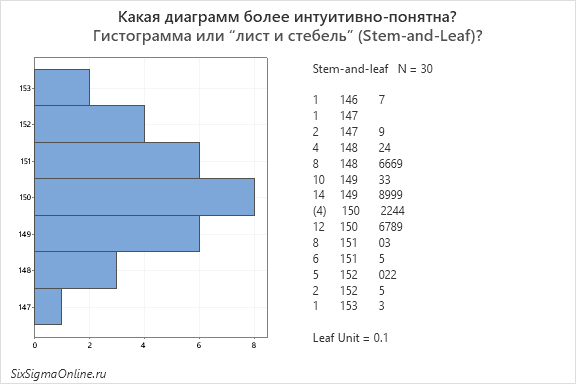
Диаграммы внешне выглядят по-разному, но отражают практически ту же информацию. “Лист и стебель” вполне подойдет для небольшого массива данных, и когда у вас нет под рукой программного обеспечения для построения гистограммы. Вот срочно вам понадобилось на производстве понять распределение наблюдений, а в кармане лишь карандаш и салфетка – рисуйте Stem-and-Leaf.
Гистограмма лучше справится с большим массивом данных и не потребует от вас округления наблюдений, так как недостаток низкого разрешения оставила своему предшественнику. Поэтому если есть возможность построить гистограмму, то выбор очевиден. Кроме того, гистограмма явно нагляднее, чем “лист и стебель”. Да что тут говорить, вы и сами все видите:
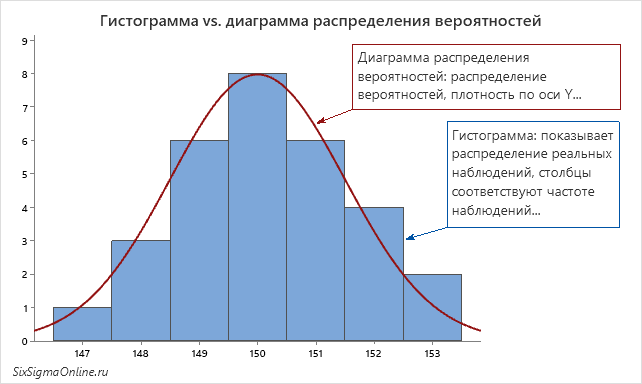
Отличие гистограммы от диаграмм распределения вероятностей (Probability Distribution Plot)
Оба графика – и гистограмма, и диаграмма распределения вероятностей – отражают распределение, только в первом случае это – распределение реальных наблюдений, а во втором – вероятностей, теоретической величины. Как следствие, гистограммы чаще всего покрыты ступенчатыми выступами, соответствующими некоему ограниченному количеству информации о распределении переменной, которое мы обладаем. Диаграмма распределения вероятностей чаще всего отображает плавную линию, соответствующую бесконечному количеству наблюдений:
Есть еще масса мелких отличий – как то: частота наблюдений по оси Y у гистограмм или плотность у диаграмм распределения вероятностей, – но они все являются лишь следствием вышеуказанных особенностей обоих графиков. Кроме того, диаграмма распределения вероятностей может применяться для решения совершенно других задач, нежели гистограмма. Подробнее в статье Диаграмма распределения вероятностей (Probability Distribution Plot).
Отличие гистограммы от диаграммы Парето (Pareto Chart)
Мне не доводилось сталкиваться со случаями, когда гистограмму не могли отличить от диаграммы Парето, но я довольно часто слышу, что диаграмма Парето состоит из гистограммы и некоторых дополнительных элементов. Это не верно. На диаграмме Парето столбцами отражены количества наблюдений в дискретных категориях, при этом колонки ранжированы по убыванию. Ее можно назвать столбчатой диаграммой, но никак не гистограммой.
Диаграмме Парето посвящена не одна публикация на нашем сайте. Попробуйте поиск по соответствующему тегу, чтобы узнать больше.
Если вы сталкивались с заблуждениями относительно гистограммы и других типов диаграмм, которые я не описал выше, буду благодарен за дополнение к статье.
Как построить гистограмму вручную?
Несмотря на то, что гистограммы легче всего построить, используя программное обеспечение, попробуем сделать это своими собственными силами. Возьмем ряд наблюдений:
3, 5, 11, 12, 19, 22, 23, 25, 27, 29, 35, 36, 37, 45, 49
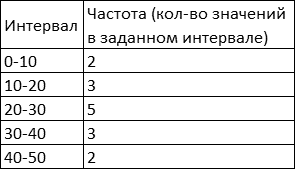
Сама по себе эта строчка несёт мало информации, но если поделить ее на удобные интервалы, то легко можно сгруппировать все данные и представить в виде следующей таблицы:
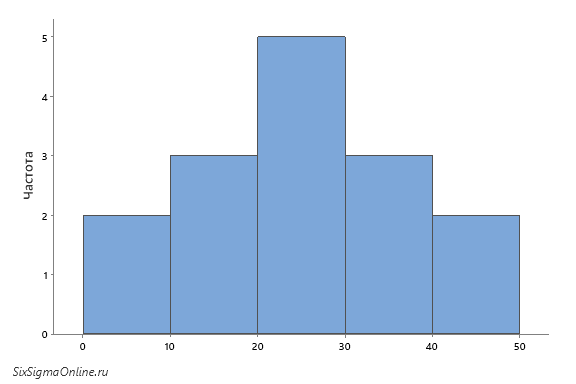
Гистограмма, построенная на данных таблицы, будет выглядеть следующим образом:
По оси Y в данном случае отложено количество наблюдений, попадающих в соответствующий диапазон на оси X.
Выбор интервалов (Binning)
Насколько удобным можно назвать выбранный выше интервал? По каким критериям определить, правильно ли он подобран? И как выбор интервала может повлиять на интерпретацию гистограммы? Все это рассмотрим ниже.
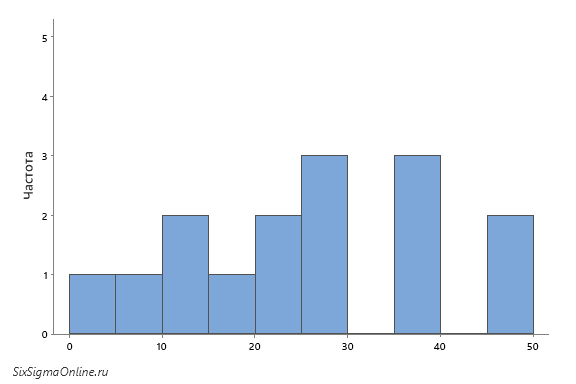
Предположим, вместо пяти отрезков по 10 единиц мы поделим весь диапазон на десять отрезков по 5 – интервалы станут в два раза короче. В таком случае гистограмма примет следующий вид:
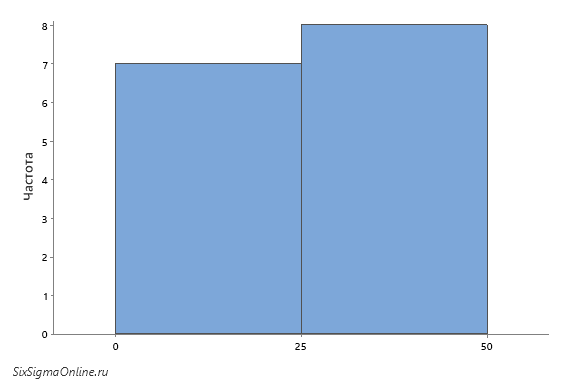
…или всего на 2 интервала – от 0 до 25 и от 25 до 50:
Становится понятно, что один и тот же набор данных может выглядеть совсем по-разному, будучи представленным в виде гистограммы. Определение величины интервала (длинны отрезка по оси X) играет ключевую роль как для визуализации данных, так и для корректности отображаемой информации. При этом подбор диапазонов может не только выявить скрытую информацию о наблюдаемой величине (характеристике процесса), но и сыграть злую шутку, скрыв важную информацию или натолкнув на ложное предположение.
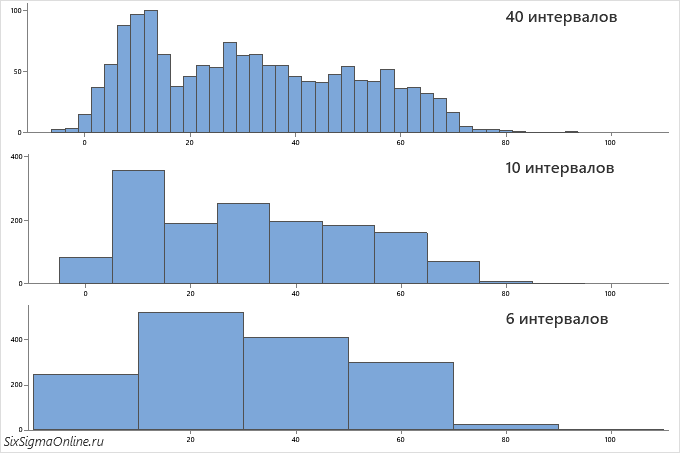
Пример ниже отчетливо иллюстрирует, как распределение наблюдаемой величины, содержащее три моды – пика, – может быть “удачно” замаскировано изменением величины интервалов:
Как же выбрать верный интервал?
К сожалению, для выбора интервалов нет единого верного подхода. Вместо этого есть несколько рекомендаций. К примеру, одна из наиболее общих рекомендаций советует нам разделить весь диапазон наблюдений на 5-30 интервалов. Согласитесь, смысл в этом есть, однако мы уже видели, к чему приводит изменение количества интервалов, а подбирать вручную одну из 25 возможностей – не самая легкая задача. Тем более, что для большого количества данных может понадобиться и больше интервалов.
Еще одна рекомендация говорит, что мы должны поделить весь диапазон так, чтобы в каждый интервал попадало не менее 5-10 наблюдений. Опять же, что делать, когда данных много? И что делать, если в данных есть прореха: например, в один из интервалов не попадет ни одно значение, хотя в интервалах по соседству их будет предостаточно? Разумеется, и в этом случае придется перебрать несколько вариантов, прежде чем мы найдем верный.
Существуют также различные формулы, которые через степени, корни и логарифмы помогут вам найти то самое правильное количество интервалов. Какая формула дает верный результат? При каком расчете от вас не ускользнут нужные детали на графике? Или в каждом случае перебирать все варианты?
Рекомендаций и вариантов расчета гораздо больше, чем нам хотелось бы потратить времени на построение одного графика. Поэтому, к сожалению, вынужден констатировать тот факт, что на практике все либо полагаются на программное обеспечение, либо на собственную “чуйку”, перебирая несколько вариантов вручную и обосновывая это разумными соображениями.
В первом случае, при использовании специализированного ПО, есть хотя бы надежда, что в нем заложен некий алгоритм выбора оптимального количества интервалов. Во втором – при ручном подборе количества интервалов – я не стану утверждать, что опыт не может подсказать, как подобрать верное количество интервалов. Лишь замечу, что от вас все еще может что-то ускользнуть. Как минимум ваше время. Но если вы все же решили заняться подбором количества интервалов вручную и посмотреть, как от этого меняется внешний вид гистограммы, ниже я расскажу вам, как это сделать быстрее всего.
На мой взгляд, первый способ более прагматичен. Строить графики с помощью ПО быстрее и комфортнее, чем в ручном режиме. Коррекция со стороны исследователя иногда необходима, но не обязательна. Нужно позволить программе делать свою работу, а исследователю свою: вместо того, чтобы корпеть над одним графиком, не забывайте:
Как построить гистограмму в пакете “101 инструмент вашего проекта шести сигм”?
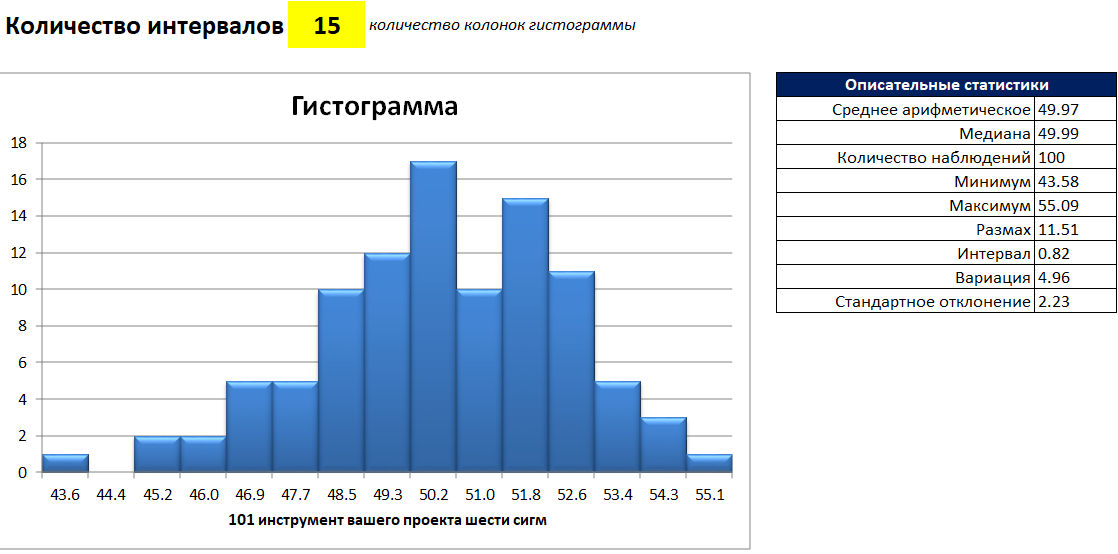
Для построения гистограмм в пакете “101 инструмент вашего проекта шести сигм” откройте папку Measure и выберите инструмент №33 – Histogram. Вам потребуется внести все наблюдения в колонку “B”, и как только это будет сделано, ваша гистограмма готова:
Также обратите внимание на опцию выбора количества интервалов непосредственно над диаграммой. Помните, выше я обещал показать, как сделать ручной подбор наиболее быстрым? Так вот это и есть тот способ. Просто меняйте значение в желтой ячейке от 5 до 30 и следите за тем, как меняется ваша гистограмма.
Как построить гистограмму в Minitab?
Большинство пакетов статистической обработки данных, и Minitab тому не исключение, содержат встроенную функцию и алгоритм построения графиков. С их помощью вся процедура превращения числового ряда в гистограмму сводится к нескольким кликам мышью. С другой стороны, упрощение процесса создания диаграмм – не главное достоинство специализированной программы. Что еще может предложить нам программная среда? Рассмотрим ниже.
Для того, чтобы построить гистограмму, программе необходимы данные – результаты наблюдений, желательно выстроенные в столбик с заголовком-названием. В противном случае построенный график будет иметь название, например, “Hystogram of С1” (где С1 – столбик, в котором размещены данные). Согласитесь, не очень-то информативно. К тому же, если построение гистограммы является частью проекта, то с его расширением разобраться, какая именно гистограмма представляет нужные нам результаты, будет всё труднее.
Как внести данные на рабочий лист программы, читайте в заметке “Заносим” данные: 4 способа. В этой публикации особенности внесения данных упущены – будем считать, что данные уже заданы, и перейдем непосредственно к процессу построения гистограммы.
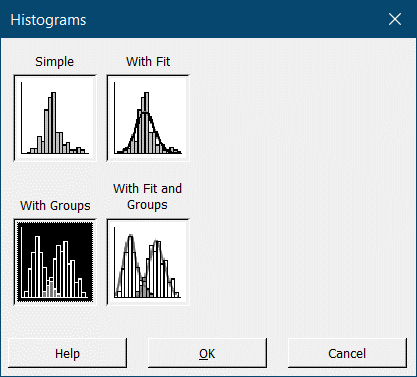
Чтобы построить гистограмму, в меню Graph выберите пункт Histogram. Эта команда откроет окно, которое предложит нам выбрать одну из четырех возможностей:
Выглядит следующим образом:
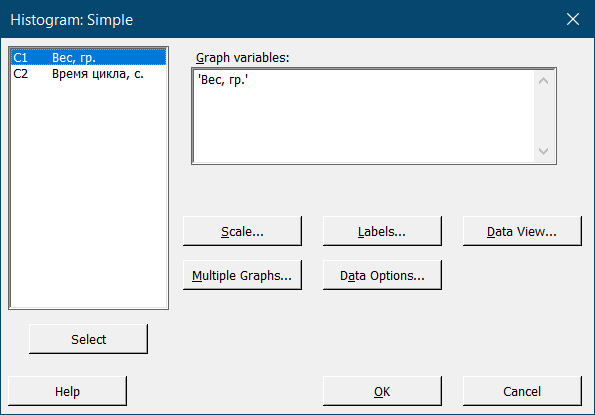
Выделенная по умолчанию иконка – Simple или обычная гистограмма – позволит построить простейшую гистограмму. Нажимаем OK, чтобы перейти в следующее меню:
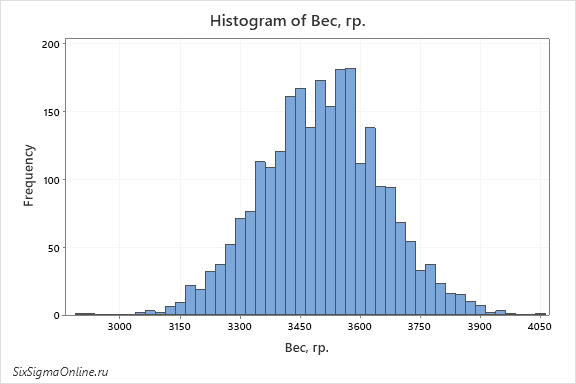
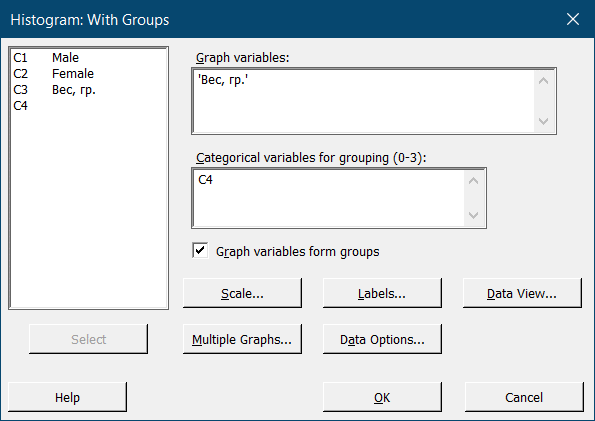
В поле Graph variables можно указать один или несколько столбцов с данными сразу. Для этого нужно дважды кликнуть на нужный столбик в поле слева или выбрать его одним кликом мыши и нажать Select. Как только название столбика появится в поле Graph variables, мы знаем, что нужные данные были заданы. Теперь, чтобы построить гистограмму, достаточно нажать OK:
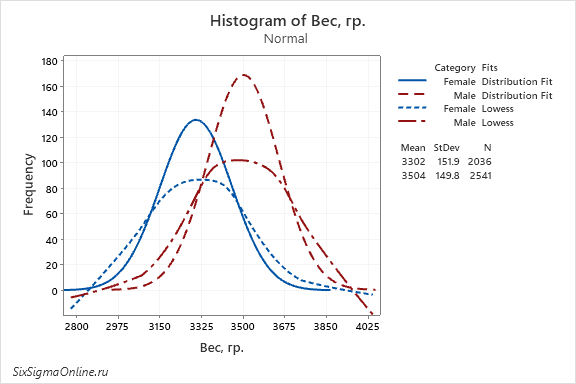
При выборе гистограммы с наложением кривой распределения вероятностей – With Fit – получим гистограмму, на которую будет наложена (по умолчанию) кривая нормального распределения. Если нам известно, что закон распределения отличается от нормального, то в окне настройки гистограммы можем задать функцию, с помощью которой следует аппроксимировать результаты наблюдений. Для этого в окне настроек выберите опцию Data View:
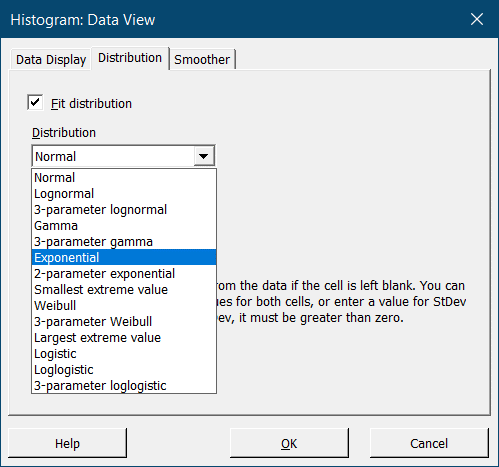
В закладке Distribution следующего меню установите флажок напротив Fit Distribution и выберите необходимый вид распределения в появившемся списке:
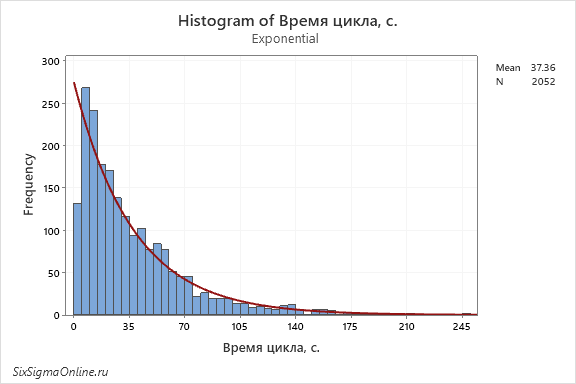
Программа автоматически аппроксимирует данные (в рассмотренном примере выбрано экспоненциальное распределение):
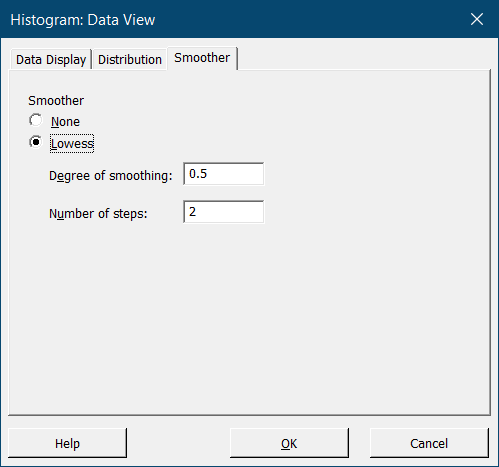
Мы также можем наложить на гистограмму сглаживающую кривую. Для этого выберите опцию Data View еще раз и в появившемся окне перейдите на закладку Smoother. Установите флажок напротив Lowess – это название алгоритма, который использует программа:
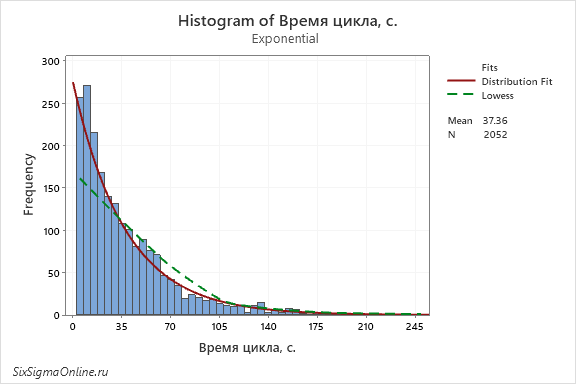
Параметры сглаживания – степень и количество шагов – оставляем по умолчанию: 0.5 и 2 соответственно. Полученная гистограмма выглядит следующим образом:
Варьируя этими значениями (степень сглаживания в пределах от 0 до 1), можно менять плавность, мягкость перепадов, приближённость к данным сглаживающей кривой, в зависимости от наших данных и цели анализа.
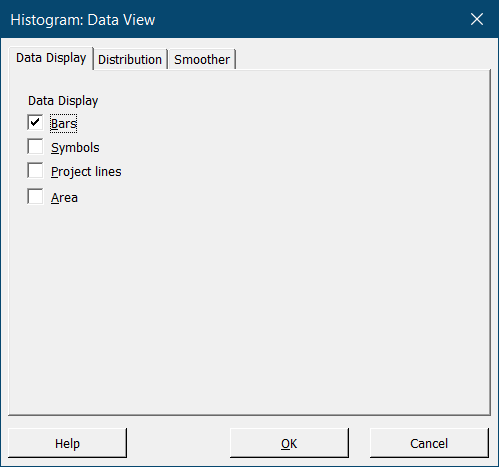
На вкладке Data Display окна Histogram: Data View можно выбрать различные, относительно нестандартные, способы представления данных на гистограмме:
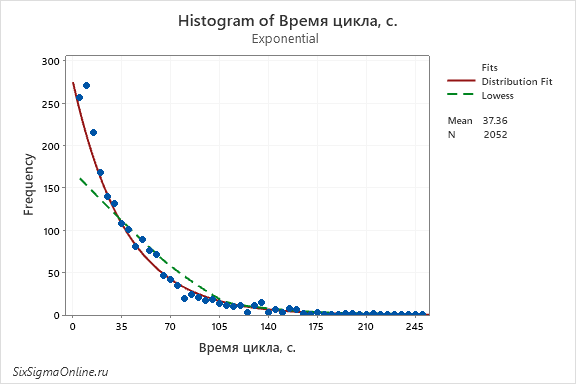
Если вместо значения по умолчанию – Bars” (колонки) – установить флажок напротив Symbols (символы), частота появления наблюдений в каждом интервале будет представлена виде точек:
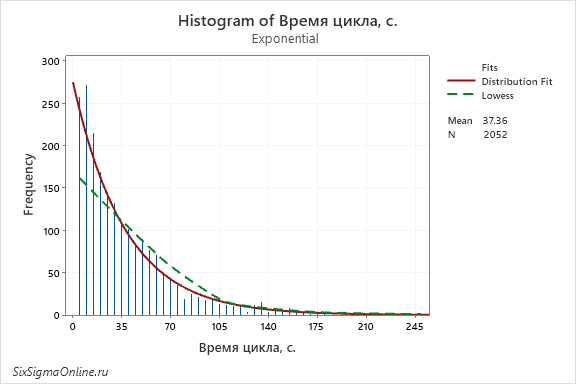
Опция Project lines (линии проекции) – позволяет представить данные в виде штрихов с длиной, соответствующей частоте появления значения (на оси X):
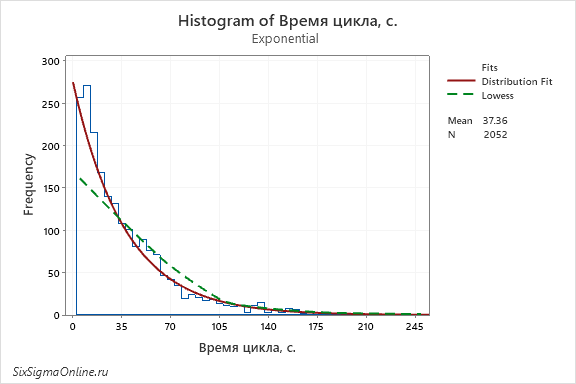
Опция Area (площадь) объединяет все прямоугольники данных, образуя единую площадь под кривой, очерченную контуром:
Обратите внимание, что флажки можно отмечать как по отдельности, так и в любых комбинациях. В таком виде гистограмма менее наглядна и, возможно, на первый взгляд покажется не столь понятной. С другой стороны, использование точек, к примеру, позволяет оценить, насколько точно данные аппроксимированы кривой распределения, а с помощью проекционных линий и обрамленных областей сравнить несколько массивов данных гораздо проще, чем с помощью стандартных “столбчатых” гистограмм.
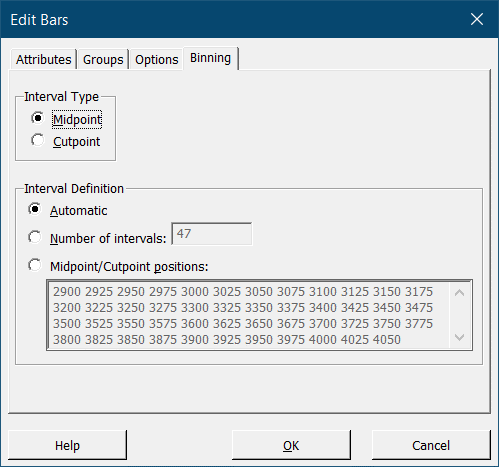
Кроме стандартных настроек, общих для всех графиков в Minitab (таких как настройка шкалы осей, цветов отдельных элементов графика, линий и границ), следует отметить настройку интервалов – Binning. Эта опция специфична для гистограмм. Чтобы перейти к настройке интервалов, дважды кликните на диаграмму – откроется окно редактирования графика. В нем следует дважды кликнуть либо по самой гистограмме, либо по оси данных (X). В открывшемся окне необходимо перейти на вкладку Binning:
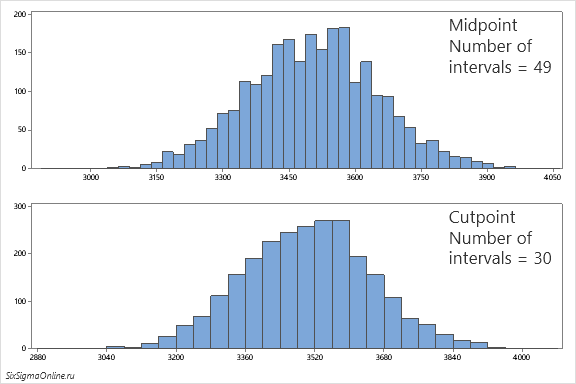
Настройки по умолчанию: Interval Type – Midpoint (значения по оси X будут расположены в центре частотных ячеек); Interval Definition – Automatic (количество интервалов определяется программой). Выбав Cutpoint в поле Interval Type, мы сдвигаем интервалы данных таким образом, что значения по оси X будут лежать в точках состыковки прямоугольников – интервалов данных, а установив флажок напротив Number of intervals в поле Interval Definition, можем задать необходимое количество интервалов для гистограммы.
Сравните: вместо Midpoint выбрана опция Cutpoint, а количество интервалов изменено с 47 по умолчанию до 30:
Как проводить анализ гистограмм?
Гистограммы нужны для того, чтобы наглядно представить распределение наблюдений. Но что еще мы можем увидеть, рассматривая прямоугольники, составляющие этот график? Какую информацию можем “прочесть”? На что обратить внимание и как это лучше сделать?
Визуальная оценка гистограмм позволяет воспринять ряд статистических показателей:
Все это постараемся разобрать ниже.
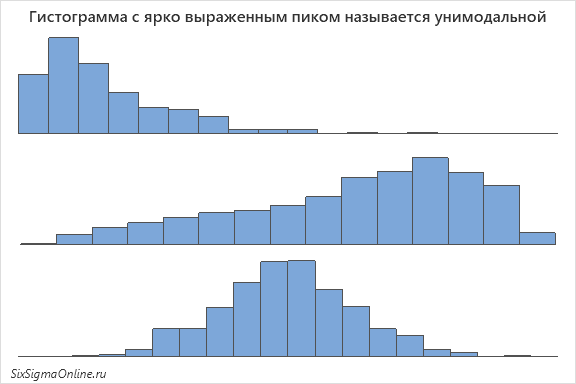
Как уже неоднократно упоминалось в этой публикации, первое, что мы будем оценивать, глядя на гистограмму – это распределение наблюдений. Тут нет ничего сложного: мы просто визуально оцениваем, на какое из известных нам распределений похожа форма нашего графика. В проектах шести сигм чаще всего сравнивают сходство с нормальным законом распределения. Визуально оценивать согласие с любым другим законом сложно, но если вы возьметесь за это, посмотрите, как могут выглядеть различные Типы распределений и соответствующие им гистограммы.
Гистограмма позволяет анализировать частотное распределение числового ряда, а соответственно дает возможность выделить наиболее вероятные число или интервал с наибольшим количеством наблюдений – другими словами, пик. Гистограмма с ярко выраженным пиком называется унимодальной:
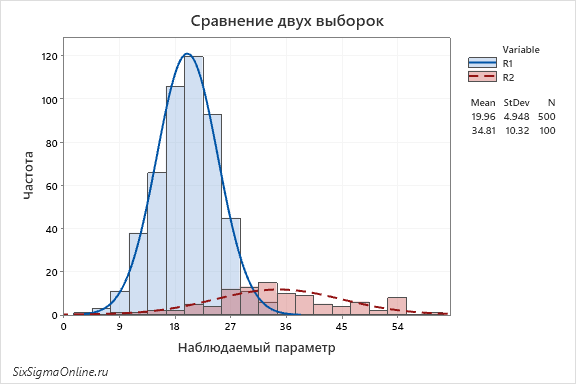
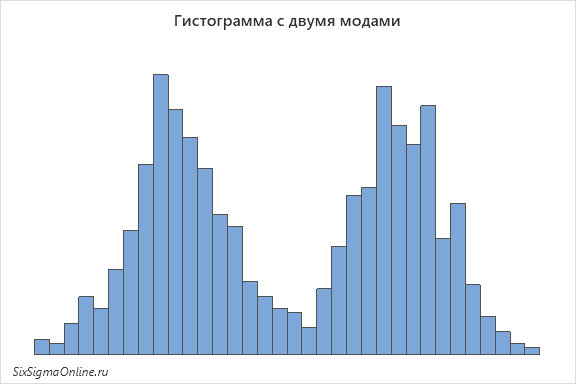
Если мы можем различить у гистограммы два ярко выраженных пика, то гистограмма называется бимодальной. Во многих случаях это значит, что выборки происходят из двух разных популяций, так как наличие двух мод в одной популяции – маловероятное явление или присущее лишь некоторым процессам. Примеры таких процессов можно найти в публикациях О бимодальном распределении и полиэтилене низкого давления и Как получить бимодальное распределение?
Гистограмма с двумя модами может выглядеть следующим образом:
И если вы получаете такое распределение по результатам входящего контроля качества, то, вероятнее всего, ваш поставщик отбирает лучшие детали, а вам посылает все остальное. Эта практика часто применяется в электронной промышленности: поставщик производит электронные компоненты, а на выходе своего процесса разделяет их на несколько групп в зависимости от того, насколько близко значение к номиналу.
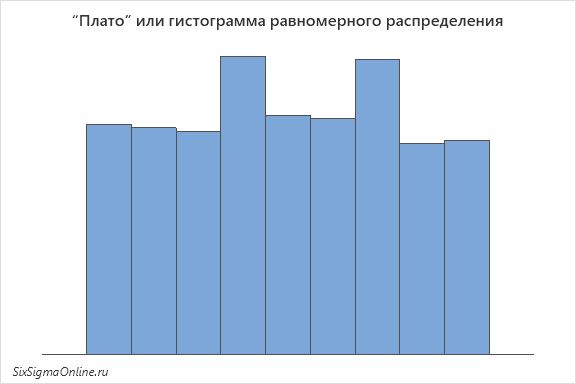
Гистограммы с тремя и большим количеством пиков (многомодальные) встречаются крайне редко и, зачастую, также свидетельствуют о присутствии специальных факторов, влияющих на исследуемую систему или процесс. Частный случай такого распределения – “плато” или гистограмма, каждый интервал которой содержит примерно равное количество значений. Такая гистограмма называется однородной или гистограммой равномерного распределения:
И если вы получаете такое распределение по результатам входящего контроля качества, то, вероятнее всего, ваш поставщик отбирает для вас лучшие детали, а все остальное посылает конкурентам.
Кроме количества пиков на гистограмме можно оценить его положение или симметрию. Гистограмма называется симметричной, если она имеет симметричную форму относительно центральной линии (правая и левая стороны одинаковой формы). Ассиметричные гистограммы бывают со скосом влево или вправо от осевой линии.
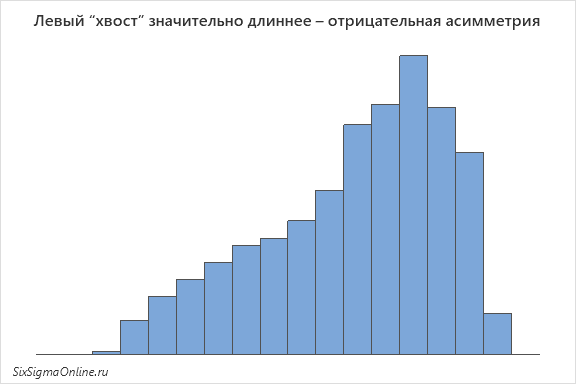
Если левая сторона гистограммы вытянута значительно больше, чем правая (или левый “хвост” значительно длиннее правого), то говорят, что гистограмма имеет отрицательную асимметрию:
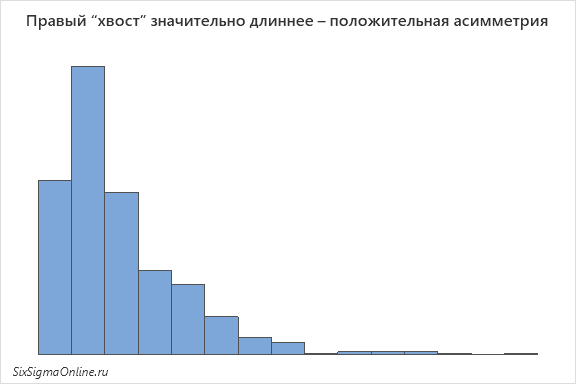
Соответственно, у гистограммы с положительной асимметрией больше в сторону выдаётся правая сторона (или правый “хвост” значительно длиннее левого):
Как представить данные на гистограмме?
Представление данных в виде диаграмм и графиков преследует одну цель: подать информацию в наглядном и понятном виде. Таким образом, важнейшими характеристиками любых диаграмм являются информативность и доступность тех данных, которые представлены с их помощью.
Несмотря на то, что гистограмма является достаточно простым и легким для восприятия графиком, представление данных с ее помощью требуют от исследователя определенного опыта, а от постороннего человека – понимания принципов построения и анализа гистограмм. Само собой разумеется, что гистограмма, построенная “своими руками”, будет понятна вам, но для человека, не знакомого с результатами наблюдений (или процессом, который описывают результаты наблюдений), ваш график может показаться не столь очевидным. Насколько построенная вами гистограмма будет информативна и понятна стороннему наблюдателю, определяет в конечном итоге то, как будет воспринята информация, которую вы показываете с ее помощью.
Как же построить такую гистограмму, которая гарантирует, что преподносимая с ее помощью информация, будет понятна всем?
Во-первых, не следует пренебрегать атрибутами стандартного графика: название гистограммы, величины и размерности осей X и Y – это первое, на что обращает внимание опытный исследователь. В этой публикации вы можете найти несколько примеров того, как гистограмма обращала ваше внимание на данные:
И того, как гистограмма заставляла вас совершенно забыть о данных, воспринимая ее лишь как иллюстрацию сказанному:
Во-вторых, представляя данные в виде гистограммы, вы должны быть уверены, что этот тип диаграмм наилучшим образом отражает ту информацию, которую вы пытаетесь показать. К примеру, разница между столбчатой диаграммой (Bar Chart) и гистограммой базируется в основном на различии представляемых типов данных. Выше мы подробно рассмотрели отличие гистограмм от других графиков. Надеюсь, это вам поможет понять, когда гистограмма не подойдет для представления имеющихся у вас данных.
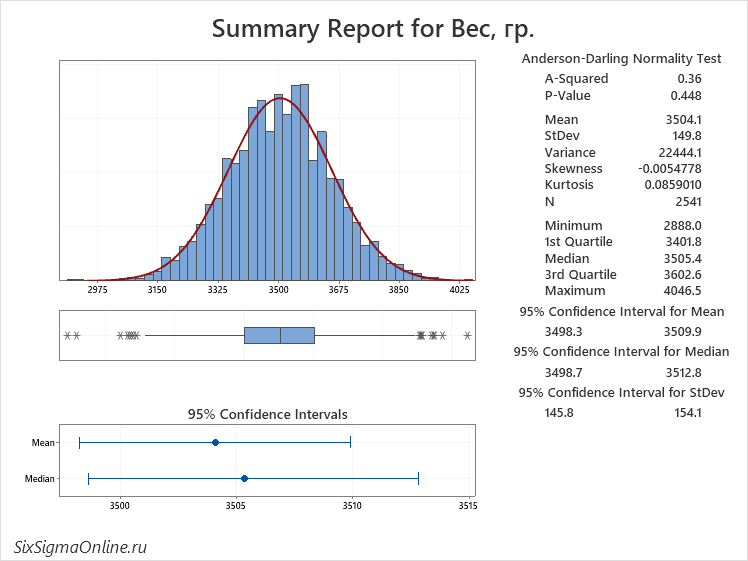
В-третьих, не пренебрегайте дополнительными возможностями программного обеспечения. Большинство пакетов статистической обработки данных содержит встроенную функцию расчета описательных статистик и вывода графического отчета. В Mintab выберите Stat \ Basic Statistics \ Graphical Summary, чтобы получить такой график:
Глядя на полученный результат, вы можете увереннее интерпретировать данные:
Как сравнивать разные массивы данных с помощью гистограмм?
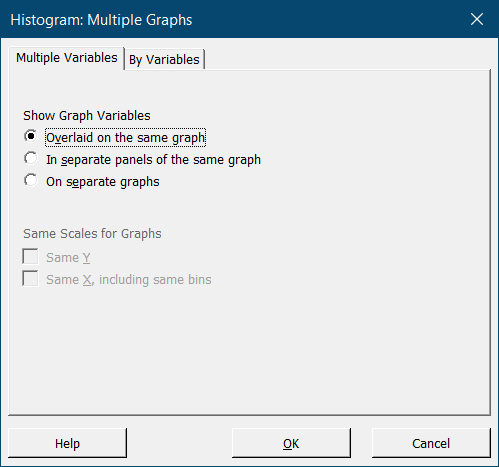
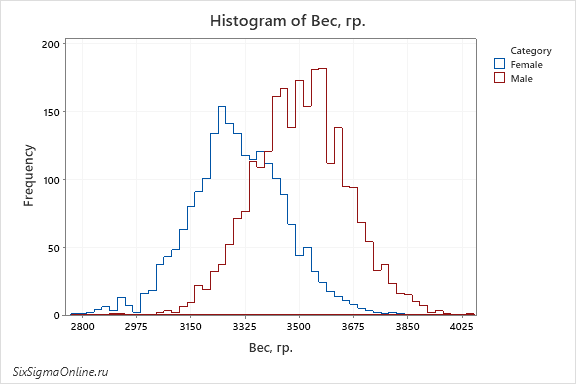
Выше мы рассмотрели общие принципы построения гистограмм и некоторые тонкости представления данных с их помощью. В этом разделе мы разберем, как сравнить гистограммы двух и более групп данных в Minitab.
Может показаться очевидным, но для того, чтобы сравнивать гистограммы различных групп данных, они должны быть:
Этого можно добиться несколькими путями в Minitab:
Этот способ подойдет, когда вам необходимо сравнить данные в разных колонках. Если же несколько массивов данных находятся в одной колонке (а именно в таком виде чаще всего удается получить результаты из базы данных производственной системы), используйте третий вариант.
Все остальные настройки и способы кастомизации, специфические для гистограмм и общие для всех графиков в Minitab, также доступны. Этого спектра более чем достаточно для сравнения данных и визуализации ваших выводов. Однако вы должны понимать, что происхождение данных, что они обозначают и цели анализа программе неизвестны. Именно поэтому настройка и оформление гистограмм проводится вручную. Множество дополнительных опций, в том числе изменение цветовых гамм, типов и толщины линий, изменений форм и размеров фигур, являются, безусловно, очень полезными при построении и оформлении гистограмм. Главное – не переусердствовать и всегда сохранять понимание того, что является одним из основных преимуществ гистограмм – простота и доступность понимания как для вас, так и для того, кому вы её представляете.
______________________________________
1 Подробнее о типах данных, а также отличии атрибутивных от непрерывных данных читайте в статье Типы данных.
2 Статистически грамотнее было бы сказать, что мы не можем отклонить гипотезу о подчинении распределения наблюдений нормальному закону. В тексте статьи использовано не совсем точное, однако более понятное выражение, которое отнюдь не меняет полученный вывод. Прим. ред.
3 На самом деле внешний вид будет зависеть от версии Minitab, которую вы используете. Прим. ред.