в практике статистики коэффициент парной корреляции может принимать следующие значения
«Ряды динамики»
106. Укажите, какой способ обработки рядов динамики применяется для изучения сезонности производства на предприятиях лесного комплекса графическим методом, именуемым сезонной волной:
• Метод приведения к одному основанию, когда за базу принимается средний уровень
107. Урожайность пшеницы в 1998 году составила 16 ц/га. Прирост урожайности в 2001 году по сравнению с 1998 составил 11,2%, а в 2002 по сравнению с 2001 урожайность составила 98,9%. Урожайность пшеницы в 2002 году = ____________________ (с точностью до 0,1 ц/га)
• 17,6 ц/га
108. Урожайность пшеницы в 2002 году = ____________________ (с точностью до 0,1), если известно, что прирост урожайности в 2002 году по сравнению с 1995 составил 11,2%, а ее абсолютное значение в 1995 году было равно 17,8 ц с гектара.
• 19,8 ц/га
109. Урожайность пшеницы в 2002 году составила 17,6 ц/га. Прирост урожайности в 2001 году по сравнению с 1997 составил 11,2%, а в 2002 по сравнению с 2001 урожайность составила 98,9%. Урожайность пшеницы в 1997 году = ____________________ (с точностью до 1 ц/га)
• 16,0 ц/га
«Корреляционный метод»
111. Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты:
• ассоциации
114. На наличие умеренной прямой линейной зависимости между признаками x и y указывает следующее значение коэффициента корреляции:
• rxy = 0,6
117. Связь между признаками является функциональной, если значение линейного коэффициента корреляции равно __________________.
• 1
«Выборочное наблюдение»
119. Если при отборе попавшая в выборку единица не возвращается в совокупность, то такой метод называется:
• бесповторный отбор
120. Какой из видов несплошного наблюдения является основным, главным:
• Выборочное наблюдение
7.24. По представленным в таблице данным, определите среднегодовой темп прироста: 1 – 40; 2 – 60; 3 – 90. 20.
8.6. В практике статистики коэффициент парной корреляции может принимать следующие значения. 0; 0,9.
8.7. Согласно теории статистики при оценке значимости уравнения регрессии и его параметров используют следующие категории. F-критерий, t-критерий.
8.8. Согласно теории статистики множественный коэффициент корреляции характеризуют следующие утверждения. отражает связь признака с остальными признаками, рассматриваемыми совместно; принимает значения в интервале.
8.9. Согласно теории статистики коэффициент корреляции Пирсона характеризуют следующие утверждения. характеризует закон распределения признака, показывает наличие линейной связи между признаками.
8.10. Согласно теории статистики можно утверждать о наличии сопряженности между двумя альтернативными признаками при следующих значениях коэффициентов. коэффициент контингенции >0,7; коэффициент контингенции > 0,5.
8.13. Если линейный коэффициент корреляции имеет положительное значение, то значение коэффициента регрессии. положительное.
8.14. Коэффициент детерминации представляет собой долю. дисперсии зависимой переменной, объясняемой регрессией в общей дисперсии.
8.15. Коэффициент регрессии а означает. на сколько в среднем изменится Y при изменении X на 1%.
8.19. Связь между признаками является функциональной, если значение линейного коэффициента корреляции равно. 1.
8.20. По направлению связи в статистике классифицируются на … прямые и обратные.
8.21. Определение параметров уравнения регрессии между двумя признаками является целью. регрессионного метода.
8.22. Расчет коэффициента детерминации невозможен без значения коэффициента. корреляции.
8.23. Связи в статистике по направлению бывают. прямые.
Вариант 1
1. В теории статистики понятие «статистическая
совокупность» включает множество…
1. однородных явлений, существование которых ограничено в пространстве и времени
2. возможных разрозненных объектов, подлежащих исследованию
3.элементов изучаемого явления, объединенных единой качественной основой
4. статистических признаков, характеризующих объект исследования
2. В теории статистики различают следующие из нижеперечисленных способы статистического наблюдения …
3. Аналитическая группировка применяется для …
1.характеристики взаимосвязей между изучаемыми явлениями и их признаками
2. разделения совокупности на качественно однородные типы единиц
3. характеристики структуры совокупности
4. характеристики структурных сдвигов
4. Подсчет групповых и общих итогов по показателям анализируемой совокупности называется …
1. комбинационной группировкой
2. простой группировкой
5.На оптовую базу поступила партия товара. Для проверки его качества была отобрана в случайном порядке пятидесятая часть партии. Путем тщательного осмотра каждой единицы товара определялось и фиксировалось его качество. Это обследование по полноте охвата относят к … наблюдению.
6.Индекс ____________ выражается отношением средних величин за два периода (по двум объектам).
1. произвольного состава
2. переменного состава
3. постоянного состава
4. структурных сдвигов
7. Если вариационный ряд имеет следующий вид:
8.Если известен индекс постоянного состава и индекс структурных сдвигов, то индекс переменного состава можно определить путем…
1. вычитания индекса структурных сдвигов из индекса постоянного состава
2. суммирования индекса постоянного состава и индекса структурных сдвигов
3. деления индекса постоянного состава на индекс структурных сдвигов
4. умножения индекса постоянного состава на индекс структурных сдвигов
9. Цена единицы продукции возросла на 3% при росте стоимости выпущенной продукции на 3,4%.Определите изменение объема производства.
1. увеличился на 6,5%
3. снизился на 11,83%
10.В практике статистики коэффициент парной коррекции может принимать следующие значения …
Ответ: контингенции, ассоциации
12. В теории статистики по аналитическому выражению выделяют следующие виды связей между признаками
13.В результате проведения регрессионного анализа получают функцию, описывающую. показателей.
15.Отношение уровней ряда динамики называется.
Ответ: коэффициентом роста
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Тесты для самоконтроля
1. Уравнение регрессии требует оценки достоверности, если оно построено
2) генеральным данным
4) выборочным данным (верно)
2. Достоверным (существенным) показателем связи называют тот
1) величина которого сформирована по выборочным данным
3) величина которого сформировалась под действием закономерности, имеющей место в выборочной совокупности
2) величина которого сформировалась под действием закономерности, имеющей место в генеральной совокупности (верно)
4) величина которого положительна
3. Под достоверностью в математической статистике понимают вероятность того, что значение проверяемого показателя связи
1) не равно нулю и не включает в себя величины противоположных знаков (верно)
2) сформировано под влиянием случайных факторов
4) включает в себя величины противоположных знаков
4. Оценка достоверности уравнения в целом проводится с использованием
1) t-критерия нормального распределения
3) F-критерия Фишера (верно)
2) критерия t-Стьюдента
4) критерия 
5. Если общий объем вариации равен 200, то воспроизведенная вариация равна
6. Получено уравнение парной линейной регрессии по 15 единицам наблюдения. Число степеней свободы для воспроизведенной дисперсии равно
7. Получено уравнение парной линейной регрессии по 15 единицам наблюдения. Число степеней свободы для остаточной дисперсии равно
8. Получено уравнение регрессии, описывающее зависимость между ценой и спросом на мясо. Если общий объем вариации равен 100, доля остаточной вариации в общей равна 0,19, численность выборки – 12. Чему равна несмещенная оценка воспроизведенной дисперсии:
9. Получено уравнение регрессии, описывающее зависимость между ценой и спросом на мясо. Если общий объем вариации равен 100, коэффициент детерминации – 0,64, численность выборки – 12. Чему равна несмещенная оценка остаточной дисперсии:
10. Получено уравнение регрессии, описывающее зависимость между ценой и спросом на мясо. Если общий объем вариации равен 100, коэффициент детерминации – 0,64, численность выборки – 12. Чему равно фактическое значение F-критерия Фишера:
11. Если коэффициент корреляции равен 0,6, численность выборки – 10. По выборке получено парное линейное уравнение регрессии. Чему будет фактическое значение F-критерия Фишера?
2) информации не достаточно для ответа на вопрос
12. Чему равно табличное значение критерия, который собирается применить исследователь для оценки значимости уравнения парной линейной регрессии, если численность выборки равна 15, уровень значимости – 0,05.
13. Чему равно фактическое значение t-критерия Стьюдента, если фактическое значение F-критерия Фишера равно 16? Численность выборки равна 10.
1) информации не достаточно для ответа на вопрос
14. По выборке из 18 единиц оценены параметры уравнения парной линейной регрессии. Общий объем вариации равен 100, объем вариации, воспроизведенной уравнением – 60. Чему равно фактическое значение t-критерия Стьюдента?
15. По выборке из 12 единиц оценены параметры уравнения парной линейной регрессии. Коэффициент корреляции равен 0,7. Чему равно фактическое значение t-критерия Стьюдента?
16. В каких пределах будет находиться генеральный коэффициент корреляции, если его выборочное значение равно 0,6?
2) от 0,4 до 0,8 (верно)
17. Чему равна ошибка коэффициента корреляции, если его выборочное значение равно 0,8? Численности выборки – 18.
18. В каких пределах будет находиться коэффициент полной регрессии выборочного уравнения:
если предельная ошибка этого коэффициента в 2,12 раза превышает среднюю ошибку, а выборочный коэффициент корреляции равен 0,6?
1) от 0,12 до 0,68 с уровнем вероятности суждения 95 % (верно)
3) от нуля до 0,824 с уровнем вероятности суждения 95 %
4) от нуля до 0,824 с уровнем вероятности суждения 90 %
19. В каких пределах будет находиться генеральный парный линейный коэффициент корреляции с уровнем вероятности суждения 95%, если его выборочное значение равно 0,9? Численности выборки – 18.
20. Чему должно быть равно фактическое значение t-критерия Стьюдента, чтобы с доверительным уровнем вероятности суждения 90 % была принята гипотеза о значимости условного начала уравнения регрессии: у=5+6х, оцененного по выборке из 60 единиц?
Расчет коэффициента корреляции
Методы расчета коэффициента корреляции
Размещено на www.rnz.ru
В том случае, когда причинная зависимость действует не в каждом конкретном случае, а в общем для всей наблюдаемой совокупности, среднем при значительном количестве наблюдений, то такая зависимость является стохастической. Частным случаем стохастической зависимости выступает корреляционная связь, при которой изменение средней величины результативного показателя вызвано изменением значений факторных показателей. Расчет степени тесноты и направления связи выступает значимой задачей исследования и количественной оценки взаимосвязи различных социально-экономических явлений. Определение степени тесноты связи между различными показателями требует определение уровня соотношения изменения результативного признака от изменения одного (в случае исследования парных зависимостей) либо вариации нескольких (в случае исследования множественных зависимостей) признаков-факторов. Для определения такого уровня используется коэффициент корреляции.
Линейный коэффициент корреляции был впервые введен в начале 90-х гг. XIX в. Пирсоном и показывает степень тесноты и направления связи между двумя коррелируемыми факторами в случае, если между ними имеется линейная зависимость. При интерпретации получаемого значения линейного коэффициента корреляции степень тесноты связи между признаками оценивается по шкале Чеддока, один из вариантов этой шкалы приведен в нижеследующей таблице:
Шкала Чеддока количественной оценки степени тесноты связи
| Величина показателя тесноты связи | Характер связи |
|---|---|
| До |±0,3| | Практически отсутствует |
| |±0,3|-|±0,5| | Слабая |
| |±0,5|-|±0,7| | Умеренная |
| |±0,7|-|±1,0| | Сильная |
При интерпретации значения коэффициента линейной корреляции по направлению связи выделяют прямую и обратную. В случае наличия прямой связи с повышением или снижением величины факторного признака происходит повышение или снижение показателей результативного признака, т.е. изменение фактора и результата происходит в одном направлении. Например, повышение величины прибыли способствует росту показателей рентабельности. При наличии обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с динамикой факторного признака. Например, с повышением производительности труда уменьшается себестоимость единицы выпускаемой продукции и т.п.
Формула расчета коэффициента корреляции
В теории разработаны и на практике применяются различные модификации формул для расчета данного коэффициента. Общая формула для расчета коэффициента корреляции имеет следующий вид:

Опираясь на математические свойства средней, общую формулу можно представить следующим образом, получив следующее выражение:
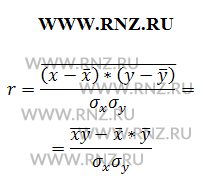
Выполняя дальнейшие преобразование, можно получить следующие формулы вычисления коэффициента корреляции Пирсона:
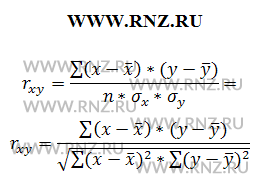
Выполняя вычисление по итоговым данным для расчета показателя корреляции, его можно рассчитать с использованием следующих формул:
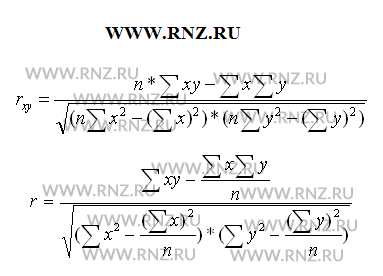
Методом расчета показателя корреляции является вычисление данного показателя с использованием его взаимосвязи с дисперсиями факторного и результативного признаков по следующей формуле:

Также показатель тесноты связи можно определить на основе его взаимосвязи с показателями уравнения регрессии, используя следующее отношение:
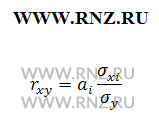
В том случае, когда rxy = 1, то это означает, что все точки (х, у) расположены на прямой и зависимость между х и у относится к функциональным. При указанном условии прямые линии регрессии совпадают. Указанное положение действует также в случае исследования трех и более показателей, если они подчинены закону нормального распределения.
Пример расчета коэффициента корреляции
Приведем пример расчета коэффициента корреляции Пирсона для значений, приведенных в следующей таблице. Для этого используем следующие данные (пример условный):
| Значение показателя X | Значение показателя Y |
|---|---|
| 1,1 | 1,3 |
| 1,9 | 1,1 |
| 1,5 | 1,2 |
| 1,9 | 0,5 |
| 1,9 | 1,5 |
| 1,1 | 1,7 |
| 0,9 | 2 |
| 1 | 0,9 |
| 1,3 | 1,2 |
| 1,5 | 1,7 |
Количество наблюдений менее 30, поэтому в нашем примере для расчета парного коэффициента корреляции используем следующую формулу:
Для этого составим вспомогательную таблицу:
| № п/п | X | Y | xy | x 2 | y 2 |
|---|---|---|---|---|---|
| 1 | 1,1 | 1,3 | 1,43 | 1,21 | 1,69 |
| 2 | 1,9 | 1,1 | 2,09 | 3,61 | 1,21 |
| 3 | 1,5 | 1,2 | 1,8 | 2,25 | 1,44 |
| 4 | 1,9 | 0,5 | 0,95 | 3,61 | 0,25 |
| 5 | 1,9 | 1,5 | 2,85 | 3,61 | 2,25 |
| 6 | 1,1 | 1,7 | 1,87 | 1,21 | 2,89 |
| 7 | 0,9 | 2 | 1,8 | 0,81 | 4 |
| 8 | 1 | 0,9 | 0,9 | 1 | 0,81 |
| 9 | 1,3 | 1,2 | 1,56 | 1,69 | 1,44 |
| 10 | 1,5 | 1,7 | 2,55 | 2,25 | 2,89 |
| Итого | 14,1 | 13,1 | 17,8 | 21,25 | 18,87 |
Полученное значение коэффициента корреляции Пирсона говорит о наличии обратной связи между X и Y. Величина коэффициента корреляции Пирсона показывает, что связь между X и Y слабая.
Онлайн калькулятор расчета коэффициента корреляции
В заключении приводим небольшой онлайн калькулятор расчета коэффициента корреляции онлайн, используя который, Вы можете самостоятельно выполнить расчет значения коэффициента корреляции Пирсона и получить интерпретацию рассчитанного значения. При заполнении формы калькулятора внимательно соблюдайте размерность полей, что позволит выполнить расчет коэффициента корреляции онлайн быстро и точно. В форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как это работает. Для определения значения показателя по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить вычисления». При заполнении формы соблюдайте размерность показателей! Дробные числа записываются с точной, а не запятой!
Онлайн-калькулятор расчета коэффициента корреляции: